|
|
@@ -3,10 +3,10 @@
|
|
|
\input{ccmbeamer}
|
|
|
%<<< title, author, institute
|
|
|
\title
|
|
|
- [Convergent Slender Body Quadrature]
|
|
|
- {Convergent Slender Body Quadrature}
|
|
|
+ [Convergent Slender Body Theory]
|
|
|
+ {Convergent Slender Body Theory}
|
|
|
%\author[Dhairya Malhotra]{ \underline{Dhairya~Malhotra}, ~{Alex Barnett}}
|
|
|
- \author[Dhairya Malhotra]{Code: {\color{blue} \url{https://github.com/dmalhotra/CSBQ}} \\
|
|
|
+ \author[Dhairya Malhotra]{Code: ~{\color{blue} \url{https://github.com/dmalhotra/CSBQ}} \\
|
|
|
\phantom{.}\\
|
|
|
\underline{Dhairya~Malhotra}, ~{Alex Barnett}}
|
|
|
|
|
|
@@ -14,15 +14,18 @@
|
|
|
%\institute{Flatiron Institute\\ \mbox{} \\ \pgfuseimage{FIbig} }
|
|
|
%\institute{\pgfuseimage{FIbig} }
|
|
|
|
|
|
- %\date[]{Code: {\color{blue} \url{https://github.com/dmalhotra/CSBQ}} \\ June 13, 2024}
|
|
|
+ %\date[]{Code: ~{\color{blue} \url{https://github.com/dmalhotra/CSBQ}} \\ June 13, 2024}
|
|
|
\date[]{June 13, 2024}
|
|
|
%>>>
|
|
|
%<<< packages
|
|
|
\usepackage{tikz}
|
|
|
- \usetikzlibrary{fit,shapes.geometric,arrows,calc,shapes,decorations.pathreplacing,patterns}
|
|
|
+ \usetikzlibrary{fit,shapes.geometric,arrows, positioning,calc,shapes,decorations.pathreplacing,patterns}
|
|
|
+ \usetikzlibrary{shadows.blur}
|
|
|
+ \usetikzlibrary{shapes.symbols}
|
|
|
\usepackage{pgfplots,pgfplotstable}
|
|
|
\pgfplotsset{compat=1.17}
|
|
|
|
|
|
+ \usepackage{graphbox}
|
|
|
\usepackage{mathtools}
|
|
|
\usepackage{multirow}
|
|
|
\usepackage{multimedia}
|
|
|
@@ -90,7 +93,6 @@
|
|
|
\begin{document}
|
|
|
\setbeamercovered{transparent}% Dim out "inactive" elements
|
|
|
|
|
|
-
|
|
|
\begin{frame}%<<< Title
|
|
|
|
|
|
\vspace{4em}
|
|
|
@@ -105,1739 +107,13 @@
|
|
|
\end{frame}%>>>
|
|
|
|
|
|
|
|
|
- \section{Introduction} %<<<
|
|
|
-
|
|
|
- \begin{FIframe}{Motivations}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1.5em}
|
|
|
- \begin{columns}[t]
|
|
|
- \column{0.5\textwidth}
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- Stokes simulations with fibers are key to modeling complex fluids
|
|
|
- (suspensions, rheology, industrial, biomedical, cellular biophysics).
|
|
|
-
|
|
|
- \only<2->{
|
|
|
- \vspace{2em}
|
|
|
- {\bf Slender Body Theory (SBT):}
|
|
|
- \begin{itemize}
|
|
|
- \item Asymptotic expansion in radius ($\varepsilon$) \\
|
|
|
- as $\varepsilon \to\ 0$ (Keller-Rubinow '76).
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- \item Doublet correction to make velocity theta-independent (Johnson '80).
|
|
|
-
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- %\vspace{1em}
|
|
|
- %The force rep w/ plain Stokeslets doesn't make velocity theta-independent on the surface, so the doublet is added to do that better.
|
|
|
- %With doublet correction , error $\sim r^2. \log(r)$.
|
|
|
- }
|
|
|
-
|
|
|
- %\only<3->{
|
|
|
- %\vspace{1em}
|
|
|
- %SBT has only very recently been placed on rigorous footing.
|
|
|
- %(Koens-Lauga '18, Mori-Ohm-Spirn '19). %(error $\sim r \log^k(r)$)
|
|
|
- %}
|
|
|
-
|
|
|
- \column{0.5\textwidth}
|
|
|
-
|
|
|
- \begin{columns}
|
|
|
- \column{0.5\textwidth}
|
|
|
- \only<1>{\embedvideo{\includegraphics[width=0.99\textwidth]{videos/starfish}}{videos/starfish.mov}}%
|
|
|
- %\starttext
|
|
|
- % \setupinteraction[state=start]
|
|
|
- % \enabletrackers[graphics.locating]
|
|
|
- % \externalfigure[sample.mov][width=10cm, height=10cm]
|
|
|
- %\stoptext
|
|
|
- \only<2->{\includegraphics[width=0.99\textwidth]{videos/starfish1}}\\
|
|
|
- Starfish larvae \\
|
|
|
- (Gilpin et al. 2016)
|
|
|
-
|
|
|
- \column{0.5\textwidth}
|
|
|
- \vspace{1em}
|
|
|
- \includegraphics[width=0.99\textwidth]{figs/oocyte} \\
|
|
|
- Drosophila oocyte (Stein et al. 2021)
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \centering
|
|
|
- \includegraphics[width=0.6\textwidth]{figs/mitosis} \\
|
|
|
- Mitotic spindle (Nazockdast et al. 2015)
|
|
|
-
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Slender Body Theory}{} %<<<
|
|
|
-
|
|
|
- {\bf Error estimates:} Rigorous analysis difficult (few very recent studies)
|
|
|
- \begin{itemize}
|
|
|
- \item classical asymptotics claims: $\varepsilon^2 \log(\varepsilon)$
|
|
|
- \item rigorous analysis: $\varepsilon \log^{3/2}(\varepsilon)$ \qquad (Mori-Ohm-Spirn '19)
|
|
|
- \item numerical tests: $\varepsilon^{1.7}$ \qquad (Mitchell et al. '21 -- verify close-touching breakdown)\\
|
|
|
- \quad close-to-touching with gap of 10$\varepsilon$,~~ only 2.5-digits in the infty-norm.\\
|
|
|
- \quad $\varepsilon$=1e-2 ~~only 1-2 digits achievable by SBT.\\
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \only<1>{
|
|
|
- \centering
|
|
|
- \includegraphics[width=0.26\textwidth]{figs/cilia.jpg}
|
|
|
-
|
|
|
- \vspace{-2ex}
|
|
|
- {\tiny Source: http://remf.dartmouth.edu/imagesindex.html}
|
|
|
- }
|
|
|
- \only<2>{
|
|
|
- \vspace{1em}
|
|
|
- \begin{columns}
|
|
|
- \column{0.5\textwidth}
|
|
|
-
|
|
|
- \begin{tabular}{| r r r|}
|
|
|
- \hline
|
|
|
- $\varepsilon$ & $\vct{u}_{exact}$ & Rel-Error \\
|
|
|
- \hline
|
|
|
- 1e-1 & 6.1492138359856e-2 & 0.5e-2 \\
|
|
|
- 1e-2 & 9.0984522324584e-2 & 0.1e-3 \\
|
|
|
- 1e-3 & 1.2015655889904e-1 & 0.2e-5 \\
|
|
|
- 1e-4 & 1.4931932907587e-1 & 0.2e-7 \\
|
|
|
- 1e-5 & 1.7848191313097e-1 & 0.3e-9 \\
|
|
|
- \hline
|
|
|
- \end{tabular}
|
|
|
-
|
|
|
-
|
|
|
- %\begin{tabular}{r r r r | c r r r r} // these are for elipse
|
|
|
- % \hline
|
|
|
- % $\varepsilon$ & $\bm u_0$ & Error \\
|
|
|
- % \hline
|
|
|
- % $0.1$ & $0.0518$ & $0.7e-2$ \\
|
|
|
- % $0.01$ & $0.0736$ & $0.2e-3$ \\
|
|
|
- % $0.001$ & $0.0950$ & $0.3e-5$ \\
|
|
|
- % $0.0001$ & $0.1163$ & $0.4e-7$ \\
|
|
|
- % %$0.00001$ & $0.1377$ & $0.6e-9$ \\
|
|
|
- % \hline
|
|
|
- %\end{tabular}
|
|
|
- % ellipse (semiaxes 2,0.5) radius eps=0.1...
|
|
|
- % N=480: L=8.578421775156826 drag force
|
|
|
- % F. = 19.17234313264176
|
|
|
- % Fexact = 19.31188135187
|
|
|
- %
|
|
|
- % ellipse (semiaxes 2,0.5) radius eps=0.01...
|
|
|
- % N=480: L=8.578421775156826 drag force
|
|
|
- % F = 13.58844162453679
|
|
|
- % Fexact = 13.59082284902
|
|
|
- %
|
|
|
- % ellipse (semiaxes 2,0.5) radius eps=0.001...
|
|
|
- % N=480: L=8.578421775156826 drag force
|
|
|
- % F = 10.52899298797188
|
|
|
- % Fexact = 10.52902479066
|
|
|
- %
|
|
|
- % ellipse (semiaxes 2,0.5) radius eps=0.0001...
|
|
|
- % N=480: L=8.578421775156826 drag force
|
|
|
- % F. = 8.594914613917958
|
|
|
- % Fexact = 8.594914990618
|
|
|
- %
|
|
|
- % ellipse (semiaxes 2,0.5) radius eps=1e-05...
|
|
|
- % N=480: L=8.578421775156826 drag force
|
|
|
- % F = 7.261368067858561
|
|
|
- % Fexact = 7.2613680720
|
|
|
- \column{0.5\textwidth}
|
|
|
- \includegraphics[width=0.95\textwidth]{figs/ring-sed}
|
|
|
- \end{columns}
|
|
|
- }
|
|
|
- %\only<3>{
|
|
|
- % \center
|
|
|
- % \vspace{-0.8em}
|
|
|
- % \includegraphics[width=0.78\textwidth]{figs/sbt-close-breakdown}
|
|
|
- %}
|
|
|
- \only<3>{
|
|
|
- \vspace{1em}
|
|
|
- {\bf Limitations of SBT:}
|
|
|
- \begin{itemize}
|
|
|
- \item no convergence analysis for fibers of given nonzero radius. %, you do not know errors in simulation .
|
|
|
- \item uncontrolled errors when fibers close $O(\varepsilon)$. %, SBT assumptions break down.
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- Efficient convergent BIE method needed, allowing adaptivity for close interactions.
|
|
|
- }
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Goals}{} %<<<
|
|
|
-
|
|
|
- Solve the slender body BVP
|
|
|
- \begin{itemize}
|
|
|
- \item in a convergent way.
|
|
|
- \item adaptively when fibers become close.
|
|
|
- \item efficiently with effort independent of radius.
|
|
|
- \end{itemize}
|
|
|
- Validate current SBT simulations.
|
|
|
-
|
|
|
- %\vspace{0.5em}
|
|
|
- %Most existing qudaratures cannot resolve high aspect ratio geometries.
|
|
|
-
|
|
|
- \vspace{4.5em}
|
|
|
- Focus on rigid fibers in this talk ~~--~~ flexible fibers for future.
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- {\em Related work:} ~~ Mitchell et al, '21 (mixed-BVP corresponding to flexible fiber loop)
|
|
|
-
|
|
|
-
|
|
|
- %Only loops for now, to avoids complications with endpoint singularities.
|
|
|
-
|
|
|
- %\textcolor{blue}{\bf Quadratures for slender bodies}
|
|
|
- %\begin{itemize}
|
|
|
- % \item compute interactions of filaments (eg. microtubules) in viscous fluids without asymptotic approximations.
|
|
|
- % \item fully resolved boundary-integral formulation; have to deal with highly anisotropic elements.
|
|
|
- %\end{itemize}
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- %\begin{FIframe}{Motivation}{} %<<<
|
|
|
- % \begin{itemize}
|
|
|
- % \item aspect ratios of $10^4$ or greater
|
|
|
- % \item existing quadrature schemes are not efficient in this regime
|
|
|
- % \end{itemize}
|
|
|
- %\end{FIframe} %>>>
|
|
|
- %\begin{FIframe}{Outline}{} %<<<
|
|
|
- %{\large
|
|
|
-
|
|
|
- % \begin{itemize}
|
|
|
- % \item Slender Body Quadrature
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % \item Stokes Mobility Problem
|
|
|
-
|
|
|
- % \end{itemize}
|
|
|
-
|
|
|
- %}
|
|
|
- %\end{FIframe} %>>>
|
|
|
-
|
|
|
- %>>>
|
|
|
-
|
|
|
-
|
|
|
- \section{Algorithms} %<<<
|
|
|
-
|
|
|
- \begin{FIframe}{Discretization}{} %<<<
|
|
|
-
|
|
|
- \vspace{-2.0em}
|
|
|
- \begin{columns}[t]
|
|
|
- \column{0.52\textwidth}
|
|
|
-
|
|
|
- {\bf Geometry description:}
|
|
|
- \begin{itemize}
|
|
|
- \item parameterization $s$ along fiber length
|
|
|
- \item coordinates $x_c(s)$ of centerline curve
|
|
|
- \item circular cross-section with radius $\varepsilon(s)$ %at each point along the centerline
|
|
|
- \item orientation vector $e_{1}(s)$
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- \only<2>{
|
|
|
- {\bf Discretization:}
|
|
|
- \begin{itemize}
|
|
|
- \item piecewise Chebyshev (order $q$) discretization in $s$ for $x_c(s)$, $\varepsilon(s)$, $e_{1}(s)$ %(either given or selected arbitrarily)
|
|
|
- \item Collocation nodes: tensor product of Chebyshev and Fourier discretization in angle with order $N_{\theta}$.
|
|
|
- \end{itemize}
|
|
|
- }
|
|
|
-
|
|
|
- \column{0.6\textwidth}
|
|
|
-
|
|
|
- \centering
|
|
|
- \only<1>{\includegraphics[width=0.99\textwidth]{figs/slender-body4}}
|
|
|
- \only<2>{
|
|
|
-
|
|
|
- \begin{tikzpicture}
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[height=0.99\textheight]{figs/slenderbody-discretization.png}};
|
|
|
- \node at (1.2, 6.3) {\Large $N_{\theta}$};
|
|
|
- \node (a) at (.7, 6) {};
|
|
|
- \node (b) at (-.0, 6) {};
|
|
|
-
|
|
|
- \node at (-1.0, 5.5) {\Large $q$};
|
|
|
- \node (d) at (.6, 8.8) {};
|
|
|
- \node (c) at (.1, 2.3) {};
|
|
|
- \draw[ultra thick, ->] (a) to [out=60,in=120, looseness=2] (b);
|
|
|
- \draw[ultra thick, ->] (c) to [out=110,in=230, looseness=1] (d);
|
|
|
- \end{tikzpicture}
|
|
|
- }
|
|
|
-
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Boundary Quadratures}{} %<<<
|
|
|
-
|
|
|
- \vspace{-0.7em}
|
|
|
- $\displaystyle u(x) ~= \int_{\Gamma} \mathcal{K}(x-y)~\sigma(y)~da(y) ~= \sum_{k=1}^{N_{panel}} \int_{\gamma_k} \mathcal{K}(x-y)~\sigma(y)~da(y)$
|
|
|
-
|
|
|
- $\displaystyle \phantom{u(x)} ~= \underbrace{\sum_{x \notin \mathcal{N}(\gamma_k)} \int_{\gamma_k} \mathcal{K}(x-y)~\sigma(y)~da(y)}_{\text{far-field}}~
|
|
|
- + \underbrace{\sum_{x \in \mathcal{N}(\gamma_k)} \int_{\gamma_k} \mathcal{K}(x-y)~\sigma(y)~da(y)}_{\text{near interactions}}$
|
|
|
-
|
|
|
- \only<2>{ %<<<
|
|
|
- \vspace{2.5em}
|
|
|
- {\bf Far field approximation:} %for $x \notin \mathcal{N}(\gamma_k)$
|
|
|
- %\vspace{0.5em}
|
|
|
- %$\displaystyle \qquad \int_{\gamma_k} \mathcal{K}(x-y)~\sigma(y)~da(y) ~\approx~
|
|
|
- % \sum_{i,j} \frac{2 \pi w_i}{N_{\theta}} \mathcal{K}(x-y(s_i,\theta_j))~\sigma(s_i,\theta_j)~J(s_i,\theta_j) $
|
|
|
-
|
|
|
- \vspace{-0.5em}
|
|
|
- \begin{columns}
|
|
|
- \column{0.5\textwidth}
|
|
|
- \begin{itemize}
|
|
|
- \item Gauss-Legendre quadrature in $s$.
|
|
|
- \item periodic trapezoidal rule in $\theta$.
|
|
|
- \item determine $\mathcal{N}(\gamma_k)$ using standard \\
|
|
|
- error estimates.
|
|
|
- \end{itemize}
|
|
|
- \column{0.6\textwidth}
|
|
|
- \resizebox{.99\textwidth}{!}{\begin{tikzpicture}
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=10cm]{figs/bernstein1.png}};
|
|
|
- \node at (4.7, 3.1) {$\mathcal{N}(\gamma_i)$};
|
|
|
-
|
|
|
- \node at (6.0, 2.45) {\textcolor{red}{$\gamma_i$}};
|
|
|
- \draw [fill=orange, fill opacity=0.35] (2.20,1.70) circle (0.7cm);
|
|
|
- \draw [fill=orange, fill opacity=0.35] (2.73,1.97) circle (0.8cm);
|
|
|
- \draw [fill=orange, fill opacity=0.35] (3.45,2.17) circle (1.0cm);
|
|
|
- \end{tikzpicture}}%
|
|
|
- \end{columns}
|
|
|
- } %>>>
|
|
|
-
|
|
|
- %\only<3>{ %<<<
|
|
|
- % % Ellipse:
|
|
|
- % %> theta=0:0.01:2*pi;
|
|
|
- % %> x=10*sin(theta);
|
|
|
- % %> y=4*cos(theta);
|
|
|
- % %> y1=y+((x).^2)*0.03;
|
|
|
- % %> hold off; imshow(I); hold on; plot(x*25+554,-y1*20+380, '.k')
|
|
|
-
|
|
|
- % \centering
|
|
|
- % \vspace{1em}
|
|
|
- % \begin{tikzpicture}
|
|
|
- % \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.7\textwidth]{figs/bernstein1.png}};
|
|
|
- % \node at (4.7, 3.1) {$\mathcal{N}(\gamma_i)$};
|
|
|
-
|
|
|
- % \node at (6.0, 2.45) {\textcolor{red}{$\gamma_i$}};
|
|
|
- % \draw [fill=orange, fill opacity=0.35] (2.20,1.70) circle (0.7cm);
|
|
|
- % \draw [fill=orange, fill opacity=0.35] (2.73,1.97) circle (0.8cm);
|
|
|
- % \draw [fill=orange, fill opacity=0.35] (3.45,2.17) circle (1.0cm);
|
|
|
- % \end{tikzpicture}~~%
|
|
|
- % \begin{tikzpicture}
|
|
|
- % \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.31\textwidth, height=0.31\textwidth]{figs/morton.png}};
|
|
|
-
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (1.655,3.80) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (1.655,2.73) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (1.655,1.65) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (2.730,3.80) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (2.730,2.73) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (2.730,1.65) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (3.805,3.80) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (3.805,2.73) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
- % \draw [fill=cyan, fill opacity=0.25] (3.805,1.65) +(-14.5pt,-14.5pt) rectangle +(14.5pt,14.5pt) ;
|
|
|
-
|
|
|
- % \draw [fill=red, fill opacity=0.99] (2.5,2.5) circle (0.09cm);
|
|
|
- % \draw [fill=orange, fill opacity=0.5] (2.5,2.5) circle (1.1cm);
|
|
|
- % \end{tikzpicture}
|
|
|
- %} %>>>
|
|
|
-
|
|
|
- % singular, near and far field evaluation
|
|
|
- % finding near-neighbors, Morton ordering, Bernstein ellipse
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Boundary Quadratures}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1em}
|
|
|
- {\bf Near interactions:} for $x \in \mathcal{N}(\gamma_k)$
|
|
|
-
|
|
|
- \vspace{0.3em}
|
|
|
- $\displaystyle \int_{\gamma_k} \mathcal{K}(x-y)~\sigma(y)~da(y) ~=~ \int_{s} \int_{\theta} \mathcal{K}(x-y(s,\theta))~\sigma(s,\theta)~J(s,\theta)~d\theta~ds$
|
|
|
-
|
|
|
- \vspace{1.5em}
|
|
|
- \begin{columns}
|
|
|
- \column{0.5\textwidth}
|
|
|
- {\bf Inner integral in $\theta$:}
|
|
|
- \begin{itemize}
|
|
|
- \item potential from a ring source \\
|
|
|
- nearly singular as $x \longrightarrow \gamma_k$.
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \column{0.47\textwidth}
|
|
|
- \resizebox{.99\textwidth}{!}{\begin{tikzpicture} %<<<
|
|
|
- \path [draw=none,fill=white!0,even odd rule] (4,0) circle (1.5) (4,0) circle (0.75);
|
|
|
- \draw[color=red, ultra thick] (0,0) ellipse (4cm and 1cm);
|
|
|
-
|
|
|
- \draw[color=blue, ultra thick] (4.7,-0.8) circle (1pt);
|
|
|
- \node at (5, -0.8) {\color{blue} \Large $x$};
|
|
|
- %\node at (5, -0.8) {\color{blue} \Large $x_i$};
|
|
|
- \node at (-4.6, 0) {\color{red} \Large $y(\theta)$};
|
|
|
- \node at (0, -0.5) {\Large $\theta$};
|
|
|
- \node (c) at (-1, -0.75) {};
|
|
|
- \node (d) at ( 1, -0.75) {};
|
|
|
- \draw[ultra thick, ->] (c) to [out=-5,in=185, looseness=1] (d);
|
|
|
- \end{tikzpicture}} %>>>
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \vspace{2em}
|
|
|
- {\bf Outer integral in $s$:}
|
|
|
- %\begin{itemize}
|
|
|
- % \item singular if $x \in \gamma_k$ with logarithmic singularity at $s = s_0$.
|
|
|
- % \item $1/|s-s_0|^{\alpha}$ decay as $|s-s_0| \longrightarrow \infty$
|
|
|
- %\end{itemize}
|
|
|
-
|
|
|
- \vspace{0.7em}
|
|
|
- \begin{tikzpicture}%<<<
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.99\textwidth]{figs/s-quad/surf.png}};
|
|
|
-
|
|
|
- \draw[color=red, ultra thick] (2.7,0.9) circle (1pt);
|
|
|
- \node at (2.5, 0.5) {\color{red} \Large $x$};
|
|
|
-
|
|
|
- \draw[ultra thick, ->] (4.3,0.45) to (3.1,0.5);
|
|
|
- \node [rotate=-6] at (5.55, 0.25) {log singularity};
|
|
|
-
|
|
|
- \draw[ultra thick, ->] (10.5,-0.25) to (12.1,-0.2);
|
|
|
- \node [rotate=-4.5] at (9.5, -0.17) {$|s-s_0|^{-\alpha}$};
|
|
|
- \end{tikzpicture}%>>>
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Fast Modal Green's Function Evaluation}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1em}
|
|
|
- \begin{columns}
|
|
|
- \column{0.7\textwidth}
|
|
|
- \begin{center} %<<<
|
|
|
- \resizebox{.99\textwidth}{!}{\begin{tikzpicture}
|
|
|
- \path [draw=none,fill=white!0,even odd rule] (4,0) circle (1.5) (4,0) circle (0.75);
|
|
|
- \only<2->{\path [draw=none,fill=blue!30,even odd rule] (4,0) circle (1.5) (4,0) circle (0.75);}
|
|
|
- \only<3->{\path [draw=none,fill=brown!80,even odd rule] (4,0) circle (0.75) (4,0) circle (0.375);}
|
|
|
- \only<3->{\path [draw=none,fill=green!80,even odd rule] (4,0) circle (0.375) (4,0) circle (0.1875);}
|
|
|
- \draw[color=red, ultra thick] (0,0) ellipse (4cm and 1cm);
|
|
|
- \only<2->{
|
|
|
- \draw[fill=black, thick] (-4,0) circle (1pt);
|
|
|
- \draw[fill=black, thick] ( 4,0) circle (1pt);
|
|
|
- \draw[fill=black, thick] (0,-1) circle (1pt);
|
|
|
- \draw[fill=black, thick] (0, 1) circle (1pt);
|
|
|
-
|
|
|
- \draw[fill=black, thick] (-2.828,-0.7071) circle (1pt);
|
|
|
- \draw[fill=black, thick] (-2.828, 0.7071) circle (1pt);
|
|
|
- \draw[fill=black, thick] ( 2.571,-0.7660) circle (1pt);
|
|
|
- \draw[fill=black, thick] ( 2.571, 0.7660) circle (1pt);
|
|
|
-
|
|
|
- \draw[fill=black, thick] (3.464,-.5) circle (1pt);
|
|
|
- \draw[fill=black, thick] (3.464, .5) circle (1pt);
|
|
|
-
|
|
|
- \draw[fill=black, thick] (3.759,-.3420) circle (1pt);
|
|
|
- \draw[fill=black, thick] (3.759, .3420) circle (1pt);
|
|
|
-
|
|
|
- \draw[fill=black, thick] (3.939,-.1736) circle (1pt);
|
|
|
- \draw[fill=black, thick] (3.939, .1736) circle (1pt);
|
|
|
-
|
|
|
- \draw[fill=black, thick] (3.985,-.0872) circle (1pt);
|
|
|
- \draw[fill=black, thick] (3.985, .0872) circle (1pt);
|
|
|
- }
|
|
|
- \only<2->{\draw[fill=blue!30,draw=none] (180:0.75)+(4,0) arc (180:0:0.75) -- (0:1.5)+(4,0) arc (0:180:1.5) -- cycle;}
|
|
|
- \only<3->{\draw[fill=brown!80,draw=none] (180:0.375)+(4,0) arc (180:0:0.375) -- (0:0.75)+(4,0) arc (0:180:0.75) -- cycle;}
|
|
|
- \only<3->{\draw[fill=green!80,draw=none] (180:0.1875)+(4,0) arc (180:0:0.1875) -- (0:0.375)+(4,0) arc (0:180:0.375) -- cycle;}
|
|
|
-
|
|
|
-
|
|
|
- \draw[color=blue, ultra thick] (4.7,-0.8) circle (1pt);
|
|
|
- \node at (5, -0.8) {\color{blue} \Large $x$};
|
|
|
- %\node at (5, -0.8) {\color{blue} \Large $x_i$};
|
|
|
- \node at (-4.6, 0) {\color{red} \Large $y(\theta)$};
|
|
|
- \node at (0, -0.5) {\Large $\theta$};
|
|
|
- \node (c) at (-1, -0.75) {};
|
|
|
- \node (d) at ( 1, -0.75) {};
|
|
|
- \draw[ultra thick, ->] (c) to [out=-5,in=185, looseness=1] (d);
|
|
|
-
|
|
|
- \end{tikzpicture}}
|
|
|
- \end{center} %>>>
|
|
|
- \column{0.3\textwidth}
|
|
|
- $\displaystyle \int_{\theta} \mathcal{K}(x-y(\theta))~\sigma(\theta)~d\theta$
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- %\vspace{-1em}
|
|
|
- %\begin{center} %<<<
|
|
|
- %\begin{tikzpicture}
|
|
|
- % \draw[color=red, ultra thick] (0,0) ellipse (4cm and 1cm);
|
|
|
- % \draw[color=blue, ultra thick] (4.7,-0.8) circle (1pt);
|
|
|
- % \node at (5, -0.8) {\color{blue} \Large $x$};
|
|
|
- % \node at (-4.6, 0) {\color{red} \Large $y(\theta)$};
|
|
|
- % \node at (0, -0.5) {\Large $\theta$};
|
|
|
- % \node (c) at (-1, -0.75) {};
|
|
|
- % \node (d) at ( 1, -0.75) {};
|
|
|
- % \draw[ultra thick, ->] (c) to [out=-5,in=185, looseness=1] (d);
|
|
|
- %\end{tikzpicture}
|
|
|
- %\end{center} %>>>
|
|
|
-
|
|
|
- %$\qquad \displaystyle \int_{\theta} \mathcal{K}(x-y(\theta))~\sigma(\theta)~d\theta ~=~ \sum_n \mathcal{K}_n(x) \widehat{\sigma_n}$
|
|
|
-
|
|
|
- %where, $y(\theta)$ is a circular source loop, and $\mathcal{K}_n(x) = \int_{\theta} e^{-in\theta} \mathcal{K}(x-y(\theta))~d\theta$ are the modal Green's functions.
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \begin{itemize}
|
|
|
- \item Analytic representation in special functions - Young, Hao, Martinsson JCP-2012
|
|
|
- \begin{itemize}
|
|
|
- \item modal Green's functions -- method of choice for axisymmetric problems.
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \only<2->{
|
|
|
- \vspace{1em}
|
|
|
- \item Build special quadrature rules!
|
|
|
- \begin{itemize}
|
|
|
- \item \eg~ generalized Gaussian quadratures: ~~Bremer, Gimbutas and Rokhlin - SISC 2010.
|
|
|
-
|
|
|
- \only<3->{
|
|
|
- \vspace{0.75em}
|
|
|
- \item Different rule for each nested annular region (up to $10^{-6}$ from source). %(and different accuracy tolerance $\epsilon$).
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \!\!\!\!\!$\sim 48$ quadrature nodes for $n_0 = 8$ ~and~ 10-digits accuracy. \\
|
|
|
- \!\!\!\!\!$\sim 26M$ modal Green's function evaluations/sec/core (Skylake 2.4GHz)
|
|
|
- }
|
|
|
- \end{itemize}
|
|
|
- }
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- %\begin{FIframe}{Fast Modal Green's Function Evaluation}{} %<<<
|
|
|
-
|
|
|
- % \vspace{-1.5em}
|
|
|
- % \begin{center} %<<<
|
|
|
- % \begin{tikzpicture}
|
|
|
- % \path [draw=none,fill=blue!30,even odd rule] (4,0) circle (1.5) (4,0) circle (0.75);
|
|
|
- % \only<2->{\path [draw=none,fill=brown!80,even odd rule] (4,0) circle (0.75) (4,0) circle (0.375);}
|
|
|
- % \only<2->{\path [draw=none,fill=green!80,even odd rule] (4,0) circle (0.375) (4,0) circle (0.1875);}
|
|
|
- % \draw[color=red, ultra thick] (0,0) ellipse (4cm and 1cm);
|
|
|
- % \draw[fill=blue!30,draw=none] (180:0.75)+(4,0) arc (180:0:0.75) -- (0:1.5)+(4,0) arc (0:180:1.5) -- cycle;
|
|
|
- % \only<2->{\draw[fill=brown!80,draw=none] (180:0.375)+(4,0) arc (180:0:0.375) -- (0:0.75)+(4,0) arc (0:180:0.75) -- cycle;}
|
|
|
- % \only<2->{\draw[fill=green!80,draw=none] (180:0.1875)+(4,0) arc (180:0:0.1875) -- (0:0.375)+(4,0) arc (0:180:0.375) -- cycle;}
|
|
|
-
|
|
|
- % \draw[color=blue, ultra thick] (4.7,-0.8) circle (1pt);
|
|
|
- % \node at (5, -0.8) {\color{blue} \Large $x$};
|
|
|
- % \node at (-4.6, 0) {\color{red} \Large $y(\theta)$};
|
|
|
- % \node at (0, -0.5) {\Large $\theta$};
|
|
|
- % \node (c) at (-1, -0.75) {};
|
|
|
- % \node (d) at ( 1, -0.75) {};
|
|
|
- % \draw[ultra thick, ->] (c) to [out=-5,in=185, looseness=1] (d);
|
|
|
-
|
|
|
- % \end{tikzpicture}
|
|
|
- % \end{center} %>>>
|
|
|
-
|
|
|
- % \vspace{-1em}
|
|
|
- % \begin{itemize}
|
|
|
- % \item Build special quadrature rule ${\color{red}(w_i, \theta_i)}$ such that,
|
|
|
-
|
|
|
- % \qquad\qquad $\displaystyle \int_{\theta} e^{-in\theta} \mathcal{K}(x-y(\theta))~d\theta ~\approx~ \sum_i {\color{red} w_i} e^{-in\theta_i} \mathcal{K}(x-y({\color{red}\theta_i}))$
|
|
|
-
|
|
|
- % for all Fourier modes ($n \leq n_0$) and all targets $x$ in the annulus.
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % \only<2->{
|
|
|
- % \item Different rule for each nested annular region (up to $10^{-6}$ from source). %(and different accuracy tolerance $\epsilon$).
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % \!\!\!\!\!$\sim 48$ quadrature nodes for $n_0 = 8$ ~and~ 10-digits accuracy. \\
|
|
|
- % \!\!\!\!\!$\sim 26M$ modal Green's function evaluations/sec/core (Skylake 2.4GHz)
|
|
|
- % }
|
|
|
- % \end{itemize}
|
|
|
-
|
|
|
- %\end{FIframe} %>>>
|
|
|
-
|
|
|
- %\begin{FIframe}{Generalized Chebyshev Quadratures}{} %<<<
|
|
|
-
|
|
|
- % \vspace{-2em}
|
|
|
- % \begin{columns}
|
|
|
- % \column{0.5\textwidth}
|
|
|
-
|
|
|
- % \begin{itemize}
|
|
|
- % \item Generate several integrands:
|
|
|
- % \end{itemize}
|
|
|
-
|
|
|
- % $\qquad\qquad f_i(\theta) = e^{-i n_{i} \theta} \mathcal{K}(x_i - y(\theta))$
|
|
|
-
|
|
|
- % \column{0.5\textwidth}
|
|
|
- % \begin{center} %<<<
|
|
|
- % \resizebox{.99\textwidth}{!}{\begin{tikzpicture}
|
|
|
- % \path [draw=none,fill=blue!30,even odd rule] (4,0) circle (1.5) (4,0) circle (0.75);
|
|
|
- % \draw[color=red, ultra thick] (0,0) ellipse (4cm and 1cm);
|
|
|
- % \draw[fill=blue!30,draw=none] (180:0.75)+(4,0) arc (180:0:0.75) -- (0:1.5)+(4,0) arc (0:180:1.5) -- cycle;
|
|
|
-
|
|
|
- % \draw[color=blue, ultra thick] (4.7,-0.8) circle (1pt);
|
|
|
- % \node at (5, -0.8) {\color{blue} \Large $x_i$};
|
|
|
- % \node at (-4.6, 0) {\color{red} \Large $y(\theta)$};
|
|
|
- % \node at (0, -0.5) {\Large $\theta$};
|
|
|
- % \node (c) at (-1, -0.75) {};
|
|
|
- % \node (d) at ( 1, -0.75) {};
|
|
|
- % \draw[ultra thick, ->] (c) to [out=-5,in=185, looseness=1] (d);
|
|
|
-
|
|
|
- % \end{tikzpicture}}
|
|
|
- % \end{center} %>>>
|
|
|
- % \end{columns}
|
|
|
-
|
|
|
- % \only<2->{
|
|
|
- % \vspace{0.25em}
|
|
|
- % \begin{itemize}
|
|
|
- % \item Build an adaptive quadrature rule $(\theta_j, w_j)$ to integrate products $f_i f_k$.
|
|
|
-
|
|
|
- % \vspace{0.75em}
|
|
|
- % \only<3->{\item Set matrix $\displaystyle A_{ij} = f_{i}(\theta_j) \sqrt{w_j}$ ~~ and compute its truncated SVD: ~~$A = U \Sigma V^{*}$.}
|
|
|
-
|
|
|
- % \vspace{0.75em}
|
|
|
- % \only<4->{\item Compute a column pivoted QR decomposition of $V^{*}$.}
|
|
|
-
|
|
|
- % \vspace{0.75em}
|
|
|
- % \only<5->{\item Select nodes corresponding to pivot columns $\{\theta_{j_1}, \cdots, \theta_{j_k}\}$ and \\
|
|
|
- % solve least squares problem for the quadrature weights.}
|
|
|
- % \end{itemize}
|
|
|
- % }
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % \only<6>{
|
|
|
- % $\approx 48$ quadrature nodes for $n_0 = 8$ ~and~ 10-digits accuracy. \\
|
|
|
- % $\approx 13M$ (complex) modal Green's function evaluations/sec/core (Skylake 2.4GHz)
|
|
|
- % }
|
|
|
-
|
|
|
- % % Chebyshev quadrature algorithm
|
|
|
- % % modal green's function evaluation rate
|
|
|
- %\end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Quadratures for Outer Integral}{} %<<<
|
|
|
- {\bf Near Interactions:} $x$ is off-surface or adjacent panel
|
|
|
- \begin{itemize}
|
|
|
- \item panel (Gauss-Lengendre) quadrature with dyadic refienement.
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \begin{tikzpicture}%<<<
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.99\textwidth]{figs/s-quad/surf.png}};
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.99\textwidth]{figs/s-quad/adap-quad.png}};
|
|
|
-
|
|
|
- \draw[color=red, ultra thick] (2.7,0.5) circle (1pt);
|
|
|
- \node at (2.7, 0.25) {\color{red} \Large $x$};
|
|
|
-
|
|
|
- \draw[ultra thick, ->] (7.1,0.1) to (5.5,0.3);
|
|
|
- \node [rotate=-4.5] at (9.5, -0.17) {dyadic ref. GL panel quad};
|
|
|
- \end{tikzpicture}%>>>
|
|
|
-
|
|
|
- \only<2->{
|
|
|
- \vspace{1em}
|
|
|
- {\bf Singular Interactions:} $x$ is on-surface
|
|
|
-
|
|
|
- \only<2>{\begin{tikzpicture}%<<<
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.99\textwidth]{figs/s-quad/adap-quad.png}};
|
|
|
-
|
|
|
- \draw[color=red, ultra thick] (2.7,0.9) circle (1pt);
|
|
|
- \node at (2.5, 0.5) {\color{red} \Large $x$};
|
|
|
-
|
|
|
- \draw[ultra thick, ->] (3.2,-0.0) to (2.8,0.65);
|
|
|
- \node [rotate=0] at (3.5, -0.25) {special quadrature};
|
|
|
- \node [rotate=0] at (3.5, -0.70) {for $p(s) \log(s) + q(s)$};
|
|
|
-
|
|
|
- \draw[ultra thick, ->] (7.1,0.1) to (5.5,0.3);
|
|
|
- \node [rotate=-4.5] at (9.5, -0.17) {dyadic ref. GL panel quad};
|
|
|
- \end{tikzpicture}}%>>>
|
|
|
- \only<3->{%<<<
|
|
|
- \begin{tikzpicture}%<<<
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.99\textwidth]{figs/s-quad/special-quad.png}};
|
|
|
- \draw[color=red, ultra thick] (2.49,0.89) circle (1pt);
|
|
|
- \node at (2.4, 0.45) {\color{red} \Large $x$};
|
|
|
- \end{tikzpicture}%>>>
|
|
|
-
|
|
|
- {\em Instead build special quadrature rules!}
|
|
|
- \begin{itemize}
|
|
|
- \item replace composite panel quadratures with a single quadrature.
|
|
|
- %\item integrand doesn't have closed form expression, but we can still generate quadrature rules!
|
|
|
- \item Separate rules for different aspect ratios ($1$ -- $10^4$ in powers of 2)
|
|
|
- \end{itemize}
|
|
|
- }%>>>
|
|
|
- }
|
|
|
-
|
|
|
- % speedup over adaptive quadrature
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- %\begin{FIframe}{Overall Algorithm}{} %<<<
|
|
|
- % %TODO: Summary
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % {\bf Discretization:} piecewise polynomial $\times$ Fourier.
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % {\bf Far-field interactions:} standard quadratures (GL $\times$ PTR) + FMM
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % {\bf Near interactions:}
|
|
|
- % \begin{itemize}
|
|
|
- % \item special quadratures for modal Green's function and singular integral in $s$.
|
|
|
- % \item dyadic refined Gauss-Legendre quadrature in $s$ for non-singular case.
|
|
|
- % \item build local correction matrix instead of computing on-the-fly.
|
|
|
- % \end{itemize}
|
|
|
-
|
|
|
- %\end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- %\begin{frame} %<<<
|
|
|
- % \centering
|
|
|
- % \huge Numerical Results
|
|
|
- %\end{frame} %>>>
|
|
|
-
|
|
|
- %\begin{FIframe}{Numerical Results - comparison with BIEST}{} %<<<
|
|
|
- % \begin{columns}
|
|
|
- % \column{0.5\textwidth}
|
|
|
-
|
|
|
- % {\bf Green's identity (Laplace):}
|
|
|
-
|
|
|
- % $\Delta u = 0$, ~~ then for ~~ $x \in \Gamma$,
|
|
|
-
|
|
|
- % \vspace{-1em}
|
|
|
- % \[ u(x) = \frac{u(x)}{2} + \StokesSL[\partial_{n} u](x) - \StokesDL[u](x) \]
|
|
|
-
|
|
|
- % \column{0.5\textwidth}
|
|
|
- % \begin{tikzpicture}
|
|
|
- % \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.99\textwidth]{figs/biest-conv}}; % R0 = 2, r = 0.5
|
|
|
- % \draw [red, ultra thick, ->|](1.15,3.35) -- (1.30,2.99);
|
|
|
- % \node at (1.65, 2.50) {\color{red} $0.5$};
|
|
|
- % \draw [red, ultra thick, ->|](2.13,1.65) -- (1.98,2.01);
|
|
|
-
|
|
|
- % \draw [red, ultra thick, ->](3.5,1.9) -- (6.1,1.9);
|
|
|
- % \node at (4.25, 2.12) {\color{red} $1.0$};
|
|
|
- % \end{tikzpicture}
|
|
|
- % \end{columns}
|
|
|
-
|
|
|
- % \only<1>{
|
|
|
- % \vspace{1em}
|
|
|
- % {\bf Boundary Integral Equation Solver for Taylor States (BIEST)\footnotemark}
|
|
|
- % \begin{itemize}
|
|
|
- % \item quadrature for general toroidal surfaces with uniform grid.
|
|
|
- % \item partition-of-unity to separate singular part of boundary integral.
|
|
|
- % \item polar coordinate transform for singular integral.
|
|
|
- % \end{itemize}
|
|
|
- % }
|
|
|
- % \only<2>{
|
|
|
- % \centering
|
|
|
- % \vspace{1em}
|
|
|
- % \begin{tabular}{r r r r | c r r r r}
|
|
|
- % \hline
|
|
|
- % \multicolumn{4}{c|}{Slender-body Quadrature} & \multicolumn{5}{c}{BIEST\footnotemark} \\
|
|
|
- % $N$ & $\left\|e\right\|_{\infty}$ & $T_{setup}$ & $T_{eval}$ & $~$ & $N$ & $\left\|e\right\|_{\infty}$ & $T_{setup}$ & $T_{eval}$ \\
|
|
|
- % \hline
|
|
|
- % 320 & 1.5e-04 & 0.032 & 0.0004 & $~$ & 507 & 2.0e-03 & 0.1319 & 0.0017 \\
|
|
|
- % 720 & 3.5e-06 & 0.094 & 0.0013 & $~$ & 1323 & 4.0e-06 & 1.4884 & 0.0042 \\
|
|
|
- % 1280 & 5.4e-09 & 0.228 & 0.0033 & $~$ & 2523 & 4.3e-09 & 6.6825 & 0.0313 \\
|
|
|
- % 2000 & 2.5e-10 & 0.501 & 0.0079 & $~$ & 4107 & 3.5e-10 & 15.4711 & 0.0862 \\
|
|
|
- % \hline
|
|
|
- % \end{tabular}
|
|
|
- % }
|
|
|
-
|
|
|
- % \footnotetext[1]{JCP 2019 - Malhotra, Cerfon, Imbert-Gérard, O'Neil ({\href{https://github.com/dmalhotra/BIEST}{\textcolor{blue}{https://github.com/dmalhotra/BIEST}}})}
|
|
|
-
|
|
|
- % % Slenderbody - Green's identity test
|
|
|
- % % N Setup Eval Error Nelem FourierOrder
|
|
|
- % % 80 3.8000e-03 2.0000e-04 1.55153e-01 2 4
|
|
|
- % % 80 5.8000e-03 2.0000e-04 5.71073e-03 2 4
|
|
|
- % % 320 2.4900e-02 4.0000e-04 6.80325e-03 4 8
|
|
|
- % % 320 3.1500e-02 4.0000e-04 1.57426e-04 4 8
|
|
|
- % % 720 8.0700e-02 1.3000e-03 2.77260e-05 6 12
|
|
|
- % % 720 9.3700e-02 1.3000e-03 3.52629e-06 6 12
|
|
|
- % % 720 1.1270e-01 1.3000e-03 3.25405e-07 6 12
|
|
|
- % % 1280 2.2890e-01 3.3000e-03 5.48754e-09 8 16
|
|
|
- % % 2000 4.3300e-01 7.8000e-03 3.79014e-10 10 20
|
|
|
- % % 2000 5.0100e-01 7.9000e-03 2.57239e-10 10 20
|
|
|
- % % 2880 8.5870e-01 1.6100e-02 2.73956e-10 12 24
|
|
|
- % % 3920 1.3213e+00 2.9200e-02 3.88062e-10 14 28
|
|
|
- % % 5120 2.0569e+00 4.8900e-02 6.05052e-10 16 32
|
|
|
- % % 5120 2.5004e+00 5.0600e-02 6.57478e-10 16 32
|
|
|
-
|
|
|
- % % BIEST - Green's identity test
|
|
|
- % % N T_setup T_eval Error M q N1 N2
|
|
|
- % % 507 0.0677 0.0017 6.7e-03 6 4 39 13
|
|
|
- % % 507 0.0669 0.0017 6.7e-03 6 4 39 13
|
|
|
- % % 507 0.1319 0.0017 2.0e-03 6 6 39 13
|
|
|
- % % 507 0.3398 0.0016 5.1e-05 6 10 39 13
|
|
|
- % % 867 0.4813 0.0017 4.1e-05 6 12 51 12
|
|
|
- % % 1323 1.4884 0.0042 4.0e-06 8 16 63 17
|
|
|
- % % 1875 4.0895 0.0177 8.7e-08 12 18 75 25
|
|
|
- % % 2523 6.6825 0.0313 4.3e-09 14 20 87 29
|
|
|
- % % 3267 10.4136 0.0581 1.1e-09 16 22 99 33
|
|
|
- % % 4107 15.4711 0.0862 3.5e-10 18 24 111 37
|
|
|
- % % 5043 22.0902 0.1253 1.0e-10 20 26 123 41
|
|
|
- % % 6075 30.8523 0.1972 4.1e-11 22 28 135 45
|
|
|
-
|
|
|
- %\end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- %%\begin{FIframe}{Numerical Results}{} %<<<
|
|
|
-
|
|
|
- %% \vspace{-1.5em}
|
|
|
- %% \begin{columns}[t]
|
|
|
- %% \column{0.66\textwidth}
|
|
|
-
|
|
|
- %% \embedvideo{\includegraphics[width=0.99\textwidth]{videos/tangle}}{videos/tangle.mov}
|
|
|
-
|
|
|
- %% \vspace{-1ex}
|
|
|
- %% \begin{columns}
|
|
|
- %% \column{0.59\textwidth}
|
|
|
- %% Exterior Laplace BVP:
|
|
|
- %%
|
|
|
- %% \quad $\displaystyle \Delta u = 0, \quad u |_{\Gamma} = 1,$
|
|
|
-
|
|
|
- %% \quad $\displaystyle u(x) \rightarrow 0 ~\text{as}~ |x|\rightarrow 0$
|
|
|
-
|
|
|
- %% \column{0.39\textwidth}
|
|
|
-
|
|
|
- %% wire radius = \\
|
|
|
- %% ~~1.5e-3~to~4e-3
|
|
|
-
|
|
|
- %% \vspace{1ex}
|
|
|
- %% wire length = 16
|
|
|
-
|
|
|
- %% \end{columns}
|
|
|
-
|
|
|
- %% \column{0.33\textwidth}
|
|
|
-
|
|
|
- %% \includegraphics[width=0.99\textwidth]{figs/tangle-cross-section-potential-laplace.png}
|
|
|
-
|
|
|
- %% \vspace{1ex}
|
|
|
- %% \includegraphics[width=0.99\textwidth]{figs/tangle-cross-section-error-laplace.png}
|
|
|
-
|
|
|
- %% \end{columns}
|
|
|
-
|
|
|
- %% % Geometry = Tangle
|
|
|
- %% % points / s / core
|
|
|
- %% % with fourier order
|
|
|
- %% % Stokes and Laplace
|
|
|
- %% % with different accuracy
|
|
|
- %% % BVP-solve
|
|
|
- %%\end{FIframe} %>>>
|
|
|
-
|
|
|
- %%\begin{FIframe}{Numerical Results - Laplace BVP}{} %<<<
|
|
|
-
|
|
|
- %% \vspace{-1em}
|
|
|
- %% \begin{columns}
|
|
|
- %% \column{0.23\textwidth}
|
|
|
- %% \quad$\displaystyle \Delta u = 0$
|
|
|
-
|
|
|
- %% \quad$\displaystyle u |_{\Gamma} = 1$
|
|
|
-
|
|
|
- %% \vspace{1ex}
|
|
|
- %% \quad $\displaystyle u(x) \rightarrow 0$ \\
|
|
|
- %% \quad as~ $\displaystyle |x|\rightarrow \infty$
|
|
|
-
|
|
|
- %% \column{0.76\textwidth}
|
|
|
- %% %\includegraphics[width=0.56\textwidth]{figs/tangle}
|
|
|
- %% \includegraphics[width=0.49\textwidth]{figs/tangle-cross-section-potential-laplace.png}
|
|
|
- %% \includegraphics[width=0.49\textwidth]{figs/tangle-cross-section-error-laplace.png}
|
|
|
- %% \end{columns}
|
|
|
-
|
|
|
-
|
|
|
- %% \resizebox{1.05\textwidth}{!}{\begin{tabular}{r r r r | r r | r r | r r}
|
|
|
- %% \hline
|
|
|
- %% & & & & & & \multicolumn{2}{c |}{1-core} & \multicolumn{2}{c }{40-cores} \\
|
|
|
- %% $N$ & $N_{panel}$ & $N_{\theta}$ & $\epsilon_{_{GMRES}}$ & $N_{iter}$ & $\left\|e\right\|_{\infty}$ & $T_{setup}~~(N/T_{setup})$ & $T_{solve}$ & $T_{setup}$ & $T_{solve}$ \\
|
|
|
- %% \hline
|
|
|
- %% 2.8e3 & 70 & 4 & 1e-02 & 4 & 4.2e-02 & 0.13 ~~~~~~(2.1e4) & 0.03 & 0.020 & 0.013 \\
|
|
|
- %% %4.9e3 & 122 & 4 & 1e-03 & 7 & 4.9e-03 & 0.23 ~~~~~~(2.1e4) & 0.16 & 0.020 & 0.027 \\
|
|
|
- %% 1.4e4 & 172 & 8 & 1e-04 & 10 & 1.0e-03 & 0.72 ~~~~~~(1.9e4) & 1.81 & 0.051 & 0.094 \\
|
|
|
- %% 3.0e4 & 252 & 12 & 1e-05 & 14 & 3.1e-05 & 1.82 ~~~~~~(1.6e4) & 12.25 & 0.091 & 2.527 \\
|
|
|
- %% 3.1e4 & 262 & 12 & 1e-07 & 20 & 2.4e-07 & 2.47 ~~~~~~(1.2e4) & 18.97 & 0.213 & 4.239 \\
|
|
|
- %% 6.5e4 & 272 & 24 & 1e-09 & 28 & 1.1e-09 & 7.74 ~~~~~~(8.4e3) & 114.05 & 0.325 & 7.136 \\
|
|
|
- %% %7.7e4 & 276 & 28 & 1e-11 & 35 & 6.6e-11 & 11.75 ~~~~~~(6.5e3) & 200.05 & 0.539 & 10.690 \\
|
|
|
- %% \hline
|
|
|
- %% \end{tabular}}
|
|
|
-
|
|
|
- %% % Tangle BVP - Laplace
|
|
|
- %% % geom gmres_tol tol N Nelem FourierOrder iter MaxError L2-error T_setup setup-rate T_solve T_setup T_solve
|
|
|
- %% % tangle50 1e-2 1e-3 2800 70 4 4 4.2e-2 9.2e-4 0.1302 21505 0.0314 0.0200 0.0131
|
|
|
- %% % tangle100 1e-3 1e-4 4880 122 4 7 4.9e-3 6.9e-5 0.2338 20873 0.1617 0.0195 0.0272
|
|
|
- %% % tangle150 1e-4 1e-5 13760 172 8 10 1.0e-3 8.5e-6 0.7216 19069 1.8098 0.0514 0.0940
|
|
|
- %% % tangle230 1e-5 1e-6 30240 252 12 14 3.1e-5 8.1e-7 1.8162 16650 12.2452 0.0905 2.5270
|
|
|
- %% % tangle240 1e-7 1e-8 31440 262 12 20 2.4e-7 8.2e-9 2.4693 12732 18.9716 0.2125 4.2385
|
|
|
- %% % tangle250 1e-9 1e-10 65280 272 24 28 1.1e-9 4.5e-11 7.7427 8431 114.0527 0.3250 7.1356
|
|
|
- %% % tangle254 1e-11 1e-12 77280 276 28 35 6.6e-11 5.5e-13 11.7547 6574 200.0480 0.5391 10.6896
|
|
|
-
|
|
|
- %%\end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - Stokes BVP}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1.5em}
|
|
|
- \embedvideo{\includegraphics[width=0.6\textwidth]{videos/tangle}}{videos/tangle.mov}
|
|
|
- \includegraphics[width=0.39\textwidth]{figs/tangle-stokes-streamlines.png}
|
|
|
-
|
|
|
- \vspace{-1.0em}
|
|
|
- \begin{columns}[t]
|
|
|
- \column{0.25\textwidth}
|
|
|
-
|
|
|
- {\bf Exterior Stokes Dirichlet BVP:}
|
|
|
-
|
|
|
- \quad $\displaystyle \Delta {\bm u} - \nabla p = 0,$
|
|
|
-
|
|
|
- \quad $\displaystyle \nabla \cdot {\bm u} = 0,$
|
|
|
-
|
|
|
-
|
|
|
- \column{0.4\textwidth}
|
|
|
-
|
|
|
- \vspace{1.2em}
|
|
|
- \quad $\displaystyle {\bm u} |_{\Gamma} = {\bm u_0},$
|
|
|
-
|
|
|
- \quad $\displaystyle u(x) \rightarrow 0 ~\text{as}~ |x|\rightarrow 0 ,$
|
|
|
-
|
|
|
- \column{0.33\textwidth}
|
|
|
-
|
|
|
- \vspace{1.2em}
|
|
|
- wire radius =
|
|
|
- ~1.5e-3~to~4e-3
|
|
|
-
|
|
|
- \vspace{0.2ex}
|
|
|
- wire length = 16
|
|
|
-
|
|
|
- %\includegraphics[width=0.99\textwidth]{figs/tangle-stokes-streamlines.png}
|
|
|
-
|
|
|
- %\vspace{1ex}
|
|
|
- %\includegraphics[width=0.99\textwidth]{figs/tangle-cross-section-error-stokes.png}
|
|
|
-
|
|
|
- \end{columns}
|
|
|
-
|
|
|
-
|
|
|
- \vspace{1.0em}
|
|
|
- {\bf BIE formulation:}\quad
|
|
|
- $
|
|
|
- \displaystyle (I/2 + D + S~/~({\color{red}2 \varepsilon \log \varepsilon^{-1}}) ) \, {\bm \sigma} = {\bm u_0}
|
|
|
- $
|
|
|
-
|
|
|
-
|
|
|
- % Geometry = Tangle
|
|
|
- % points / s / core
|
|
|
- % with fourier order
|
|
|
- % Stokes and Laplace
|
|
|
- % with different accuracy
|
|
|
- % BVP-solve
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - Stokes BVP}{} %<<<
|
|
|
-
|
|
|
- \centering
|
|
|
- \vspace{-1.5em}
|
|
|
- \includegraphics[width=0.35\textwidth]{figs/tangle-stokes-streamlines.png}
|
|
|
- \hspace{5em}
|
|
|
- \includegraphics[width=0.40\textwidth]{figs/tangle-cross-section-error-stokes.png}
|
|
|
-
|
|
|
- \resizebox{1.05\textwidth}{!}{\begin{tabular}{r r r r | r r | r r | r r}
|
|
|
- \hline
|
|
|
- & & & & & & \multicolumn{2}{c |}{1-core} & \multicolumn{2}{c }{40-cores} \\
|
|
|
- $N$ & $N_{panel}$ & $N_{\theta}$ & $\epsilon_{_{GMRES}}$ & $N_{iter}$ & $\left\|e\right\|_{\infty}$ & $T_{setup}~~(N/T_{setup})$ & $T_{solve}$ & $T_{setup}$ & $T_{solve}$ \\
|
|
|
- \hline
|
|
|
- %8.4e3 & 70 & 4 & 1e-02 & 6 & 2.1e-01 & 0.18 ~~~~~~(4.5e4) & 0.1 & 0.024 & 0.02 \\
|
|
|
- 1.5e4 & 122 & 4 & 1e-03 & 10 & 1.9e-02 & 0.33 ~~~~~~(4.4e4) & 0.7 & 0.024 & 0.05 \\
|
|
|
- %4.1e4 & 172 & 8 & 1e-04 & 16 & 1.7e-02 & 1.22 ~~~~~~(3.3e4) & 9.8 & 0.077 & 1.84 \\
|
|
|
- 9.1e4 & 252 & 12 & 1e-05 & 21 & 1.7e-04 & 3.31 ~~~~~~(2.7e4) & 61.2 & 0.197 & 5.25 \\
|
|
|
- 9.4e4 & 262 & 12 & 1e-07 & 33 & 4.1e-06 & 4.43 ~~~~~~(2.1e4) & 104.3 & 0.224 & 7.69 \\
|
|
|
- 2.0e5 & 272 & 24 & 1e-09 & 43 & 1.4e-08 & 17.70 ~~~~~~(1.1e4) & 586.0 & 0.796 & 22.94 \\
|
|
|
- 2.3e5 & 276 & 28 & 1e-11 & 54 & 4.1e-09 & 27.67 ~~~~~~(8.4e3) & 1034.2 & 1.229 & 38.85 \\
|
|
|
- \hline
|
|
|
- \end{tabular}}
|
|
|
-
|
|
|
- % Tangle BVP - Stokes
|
|
|
- % geom gmres_tol tol N Nelem FourierOrder iter MaxError L2-error T_setup setup-rate T_solve T_setup T_solve
|
|
|
- % tangle50 1e-2 1e-3 8400 70 4 6 2.1e-01 2.2e-03 0.1856 45259 0.1589 0.0248 0.0234
|
|
|
- % tangle100 1e-3 1e-4 14640 122 4 10 1.9e-02 1.0e-04 0.3313 44190 0.7745 0.0243 0.0565
|
|
|
- % tangle150 1e-4 1e-5 41280 172 8 16 1.7e-02 1.6e-05 1.2295 33575 9.8059 0.0770 1.8448
|
|
|
- % tangle230 1e-5 1e-6 90720 252 12 21 1.7e-04 9.0e-07 3.3138 27376 61.2092 0.1975 5.2584
|
|
|
- % tangle240 1e-7 1e-8 94320 262 12 33 4.1e-06 7.6e-09 4.4355 21265 104.3853 0.2241 7.6990
|
|
|
- % tangle250 1e-9 1e-10 195840 272 24 43 1.4e-08 1.1e-10 17.7085 11059 586.0695 0.7960 22.9405
|
|
|
- % tangle254 1e-11 1e-12 231840 276 28 54 4.1e-09 6.9e-12 27.6771 8377 1034.2305 1.2298 38.8589
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
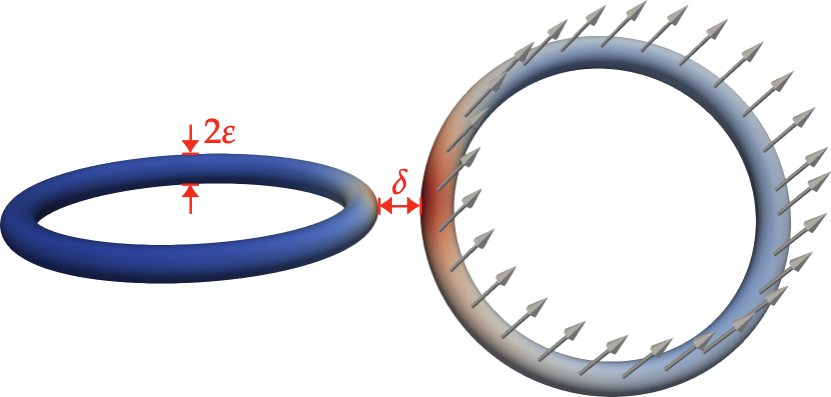
- \begin{FIframe}{Numerical Results - close-to-touching}{} %<<<
|
|
|
-
|
|
|
- \centering
|
|
|
-
|
|
|
- \only<1>{
|
|
|
- \begin{tikzpicture}
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[width=0.9\textwidth]{figs/touching.png}};
|
|
|
- \node[anchor=south west,inner sep=0] at (10,-1.7) {\includegraphics[width=0.4\textwidth]{figs/touching-zoom.png}};
|
|
|
- \draw[red,ultra thick,rounded corners] (5.75,2.55) rectangle (6.65,3.65);
|
|
|
-
|
|
|
- \draw[red,ultra thick,rounded corners] (10,-1.7) rectangle (14.98,2.95);
|
|
|
-
|
|
|
- \draw [red, ultra thick, ->|](0.7,0.7) -- (1.03,1.03);
|
|
|
- \draw [red, ultra thick, ->|](1.57,1.57) -- (1.24,1.24);
|
|
|
- \node at (1.75, 1.85) {\color{red} $0.125$};
|
|
|
-
|
|
|
- \draw [red, ultra thick, ->](3.4,2.9) -- (3.4,0.18);
|
|
|
- \node at (3.8, 1.7) {\color{red} $1.0$};
|
|
|
-
|
|
|
- \node at (7.95, 3.3) {\color{red} gap $= 0.003$};
|
|
|
- \node at (7.7, 2.8) {\color{red} $N_\theta = 88$};
|
|
|
-
|
|
|
- \end{tikzpicture}
|
|
|
- }
|
|
|
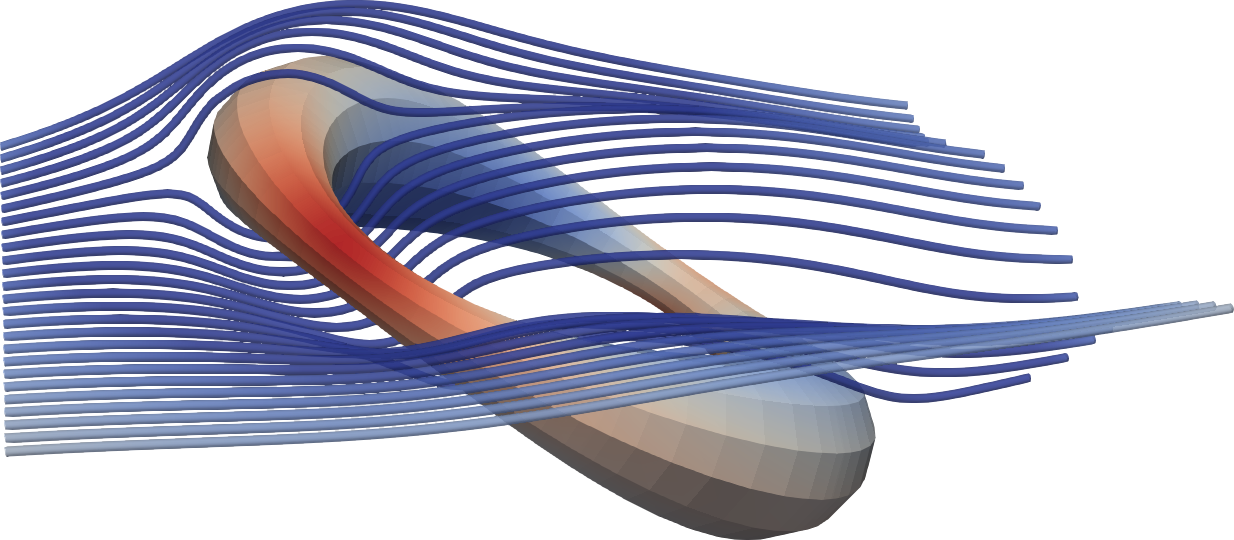
- \only<2>{
|
|
|
- \includegraphics[width=0.8\textwidth]{figs/close-to-touching-streamlines}
|
|
|
- }
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - close-to-touching}{} %<<<
|
|
|
-
|
|
|
- \centering
|
|
|
-
|
|
|
- \includegraphics[width=0.55\textwidth]{figs/touching.png}
|
|
|
- \includegraphics[width=0.4\textwidth]{figs/close-to-touching-streamlines}
|
|
|
-
|
|
|
- \begin{tabular}{r r | r r | r r | r r}
|
|
|
- \hline
|
|
|
- & & & & \multicolumn{2}{c |}{1-core} & \multicolumn{2}{c }{40-cores} \\
|
|
|
- $N$ & $\epsilon_{_{GMRES}}$ & $N_{iter}$ & $\left\|e\right\|_{\infty}$ & $T_{setup}~~(N/T_{setup})$ & $T_{solve}$ & $T_{setup}$ & $T_{solve}$ \\
|
|
|
- \hline
|
|
|
- %6.5e4 & 1e-01 & 2 & 1.3e-01 & 5.6 (1.1e+4) & 3.2 & 0.85 & 0.5 \\
|
|
|
- 6.5e4 & 1e-02 & 4 & 2.1e-02 & 8.1 (8.0e+3) & 6.5 & 1.28 & 1.4 \\
|
|
|
- %6.5e4 & 1e-03 & 7 & 1.6e-02 & 10.8 (6.0e+3) & 11.8 & 1.73 & 2.3 \\
|
|
|
- %6.5e4 & 1e-04 & 13 & 9.3e-03 & 13.6 (4.7e+3) & 22.6 & 2.13 & 4.8 \\
|
|
|
- 6.5e4 & 1e-05 & 24 & 2.4e-03 & 16.8 (3.8e+3) & 42.9 & 2.50 & 7.7 \\
|
|
|
- %6.5e4 & 1e-06 & 34 & 3.4e-05 & 19.9 (3.2e+3) & 62.5 & 2.80 & 10.9 \\
|
|
|
- 6.5e4 & 1e-07 & 43 & 2.8e-06 & 23.5 (2.7e+3) & 81.6 & 3.31 & 12.8 \\
|
|
|
- %6.5e4 & 1e-08 & 49 & 2.6e-07 & 27.4 (2.3e+3) & 96.2 & 3.72 & 14.8 \\
|
|
|
- %6.5e4 & 1e-09 & 54 & 9.3e-08 & 31.4 (2.1e+3) & 109.3 & 3.91 & 16.3 \\
|
|
|
- 6.5e4 & 1e-10 & 59 & 5.4e-08 & 35.6 (1.8e+3) & 122.9 & 4.06 & 19.2 \\
|
|
|
- %6.5e4 & 1e-11 & 64 & 5.0e-09 & 40.5 (1.6e+3) & 137.1 & 4.56 & 20.2 \\
|
|
|
- %6.5e4 & 1e-12 & 69 & 5.0e-10 & 45.6 (1.4e+3) & 152.2 & 5.00 & 22.3 \\
|
|
|
- 6.5e4 & 1e-13 & 72 & 1.3e-10 & 49.9 (1.3e+3) & 162.6 & 5.27 & 23.2 \\
|
|
|
- \hline
|
|
|
- \end{tabular}
|
|
|
-
|
|
|
- % N gmres_tol tol iter MaxError L2-error T_setup setup-rate T_solve T_setup T_solve
|
|
|
- % 64560 1e-01 1e-2 2 1.3e-01 3.2e-02 5.6700 3.1944 0.8531 0.4806
|
|
|
- % 64560 1e-02 1e-3 4 2.1e-02 2.5e-03 8.1061 6.5360 1.2818 1.3614
|
|
|
- % 64560 1e-03 1e-4 7 1.6e-02 3.1e-04 10.8099 11.8118 1.7274 2.2869
|
|
|
- % 64560 1e-04 1e-5 13 9.3e-03 2.4e-05 13.6997 22.5707 2.1291 4.8351
|
|
|
- % 64560 1e-05 1e-6 24 2.4e-03 3.7e-06 16.8026 42.8992 2.5001 7.6538
|
|
|
- % 64560 1e-06 1e-7 34 3.4e-05 2.2e-07 19.9488 62.5492 2.8044 10.8931
|
|
|
- % 64560 1e-07 1e-8 43 2.8e-06 1.4e-08 23.5213 81.6355 3.3077 12.7662
|
|
|
- % 64560 1e-08 1e-9 49 2.6e-07 1.9e-09 27.4751 96.2095 3.7236 14.7706
|
|
|
- % 64560 1e-09 1e-10 54 9.3e-08 5.5e-10 31.4113 109.2922 3.9118 16.2876
|
|
|
- % 64560 1e-10 1e-11 59 5.4e-08 2.3e-10 35.6971 122.8530 4.0588 19.2035
|
|
|
- % 64560 1e-11 1e-12 64 5.0e-09 2.2e-11 40.5914 137.0600 4.5563 20.2282
|
|
|
- % 64560 1e-12 1e-13 69 5.0e-10 2.5e-12 45.6508 152.2238 4.9972 22.3425
|
|
|
- % 64560 1e-13 1e-14 72 1.3e-10 1.5e-12 49.9494 162.6172 5.2653 23.2362
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- %>>>
|
|
|
-
|
|
|
-
|
|
|
- \section{Mobility problem} %<<<
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Mobility problem}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1em}
|
|
|
- \begin{columns}
|
|
|
- \column{0.6\textwidth}
|
|
|
-
|
|
|
- \begin{itemize}
|
|
|
-
|
|
|
- \item $n$ rigid bodies ~~$\Omega = \sum\limits_{i=1}^{n} \Omega_i$
|
|
|
-
|
|
|
- \only<1>{
|
|
|
- with velocities ~$\vct{V}(\vct{x}) = \vct{v}_i + \vct{\omega}_i \times (\vct{x}-\vct{x}^c_i)$,
|
|
|
- }%
|
|
|
- \only<2>{
|
|
|
- with velocities ~{\color{red}$\vct{V}(\vct{x}) = \vct{v}_i + \vct{\omega}_i \times (\vct{x}-\vct{x}^c_i)$},
|
|
|
- }
|
|
|
-
|
|
|
- \vspace{0.8ex}
|
|
|
- and given forces $\vct{F}_i$, ~torques $\vct{T}_i$ abount $\vct{x}^c_i$.
|
|
|
-
|
|
|
- \vspace{1.4em}
|
|
|
- \item Stokesian fluid in $\Real^3 \setminus \Omega$
|
|
|
-
|
|
|
- \vspace{0.7ex}
|
|
|
- \qquad $\displaystyle \Delta \vct{u} - \nabla p = 0, ~~\nabla \cdot \vct{u} = 0,$ \\
|
|
|
-
|
|
|
- \vspace{0.6ex}
|
|
|
- \qquad $\displaystyle \vct{u} \rightarrow 0$ ~as~ $\vct{x} \rightarrow \infty$.
|
|
|
-
|
|
|
- \vspace{1.3em}
|
|
|
- \item Boundary conditions on $\partial\Omega$,
|
|
|
-
|
|
|
- \vspace{0.6ex}
|
|
|
- \only<1>{\qquad $\displaystyle \vct{u} = \vct{V} + \vct{u}_s$.}
|
|
|
- \only<2>{\qquad $\displaystyle \vct{u} = {\color{red}\vct{V}} + \vct{u}_s$.}
|
|
|
-
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- \qquad\quad
|
|
|
- \only<1>{\phantom{\color{red} unknown: $\vct{V}(\vct{u}_i, \vct{\omega}_i)$}}
|
|
|
- \only<2>{\color{red} unknown: $\vct{V}(\vct{u}_i, \vct{\omega}_i)$}
|
|
|
-
|
|
|
- \column{0.4\textwidth}
|
|
|
- \resizebox{0.98\textwidth}{!}{\begin{tikzpicture}
|
|
|
- \node[anchor=south west,inner sep=0] at (0,0) {\includegraphics[angle=90,origin=c,width=4cm]{figs/rigid-bodies.png}};
|
|
|
-
|
|
|
- \draw[ultra thick, ->] (2.19,0.95) to (3,1.5);
|
|
|
- \node at (3.25, 1.5) {$\vct{F}_1$};
|
|
|
-
|
|
|
- \node (a) at (2.0, 1.3) {};
|
|
|
- \node (b) at (2.08, 1.3) {};
|
|
|
- \draw[thick, ->] (a) to [out=140,in=60, looseness=3] (b);
|
|
|
- \draw[ultra thick, ->] (2.1,1) to (1.85,2.15);
|
|
|
- \node at (1.85, 2.3) {$\vct{T}_1$};
|
|
|
-
|
|
|
- %\draw[color=red, ultra thick] (2.7,0.9) circle (1pt);
|
|
|
- %\node at (2.5, 0.5) {\color{red} \Large $x$};
|
|
|
-
|
|
|
- %\draw[ultra thick, ->] (4.3,0.45) to (3.1,0.5);
|
|
|
- %\node [rotate=-6] at (5.55, 0.25) {log singularity};
|
|
|
-
|
|
|
- %\draw[ultra thick, ->] (10.5,-0.25) to (12.1,-0.2);
|
|
|
- %\node [rotate=-4.5] at (9.5, -0.17) {$|s-s_0|^{-\alpha}$};
|
|
|
- \end{tikzpicture}}
|
|
|
-
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Mobility problem - double-layer formulation}{} %<<<
|
|
|
-
|
|
|
- Represent fluid velocity: ~~$\displaystyle \vct{u} = \StokesSL[\vct{\nu}(\vct{F}_i, \vct{T}_i)] + \StokesDL[{\color{red}\vct{\sigma}}] $
|
|
|
-
|
|
|
- \vspace{0.3em}
|
|
|
- and rigid body velocity: ~~$\displaystyle \vct{V} = -\sum_{i=1}^{6n} \mathfrak{v}_i \mathfrak{v}_i^T {\color{red}\vct{\sigma}}$
|
|
|
-
|
|
|
-
|
|
|
- \vspace{1.5em}
|
|
|
- Applying boundary conditions ~ ($\displaystyle \vct{u} = \vct{V} + \vct{u}_s$ ~on~ $\partial\Omega$),
|
|
|
-
|
|
|
- \vspace{0.3em}
|
|
|
- \qquad$\qquad\displaystyle
|
|
|
- (I/2 + D) \, {\color{red}\vct{\sigma}} + \sum_{i=1}^{6n} \mathfrak{v}_i \mathfrak{v}_i^T {\color{red}\vct{\sigma}} = \vct{u}_s - S \, \vct{\nu}
|
|
|
- $
|
|
|
-
|
|
|
- \vspace{0.5em}{\em(Pozrikidis - Boundary Integral and Singularity Methods for Linearized Viscous Flow)}
|
|
|
-
|
|
|
-
|
|
|
- \vspace{2em}
|
|
|
- \only<2>{
|
|
|
- Second kind integral equation, should be well-conditioned.\\
|
|
|
- What can possibly go wrong?
|
|
|
- }
|
|
|
-
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Conditioning of layer-potential operators}{} %<<<
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- \begin{columns}
|
|
|
- \column{0.05\textwidth}
|
|
|
-
|
|
|
- \column{0.35\textwidth}
|
|
|
- %\quad$\displaystyle \nabla^2 u - \nabla p = 0$ ~~in~~ $\mathbb{R}^3 \setminus \Omega$
|
|
|
-
|
|
|
- %\quad$\displaystyle u |_{\Gamma} = u_0$
|
|
|
-
|
|
|
- %\quad $\displaystyle u(x) \rightarrow 0 ~\text{as}~ |x|\rightarrow \infty$
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- $\kappa(S)$ \hfill $\sim 2.6e6$
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- $\kappa(I/2 + D)$ \hfill $\sim 4.3e6$
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- $\kappa(I/2 + D + 16 S)$ \hfill $\sim 80$
|
|
|
-
|
|
|
- \column{0.1\textwidth}
|
|
|
-
|
|
|
- \column{0.50\textwidth}
|
|
|
- \includegraphics[width=0.99\textwidth]{figs/slender-torus}
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \vspace{3em}
|
|
|
- \begin{itemize}
|
|
|
- \item For infinite cylinder (Laplace case): ~~ $\kappa(I/2 + D) ~\sim~ 1/(\varepsilon^{2} \log \varepsilon^{-1})$
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \item Combined field operator well-conditioned: ~~ $I/2 + D + S ~/~ (2\varepsilon \log \varepsilon^{-1})$
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- %\begin{FIframe}{Boundary Integral Formulation}{Dirichlet BVP} %<<<
|
|
|
-
|
|
|
- % \begin{columns}
|
|
|
- % \column{0.5\textwidth}
|
|
|
- % \quad$\displaystyle \nabla^2 u - \nabla p = 0$ ~~in~~ $\mathbb{R}^3 \setminus \Omega$
|
|
|
-
|
|
|
- % \quad$\displaystyle u |_{\Gamma} = u_0$
|
|
|
-
|
|
|
- % \quad $\displaystyle u(x) \rightarrow 0 ~\text{as}~ |x|\rightarrow \infty$
|
|
|
-
|
|
|
- % \column{0.5\textwidth}
|
|
|
- % \includegraphics[width=0.99\textwidth]{figs/biest-conv}
|
|
|
- % \end{columns}
|
|
|
-
|
|
|
- % {\bf Integral equation formulation:}
|
|
|
-
|
|
|
- % \begin{columns}
|
|
|
- % \column{0.75\textwidth}
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % $u = \frac{\sigma}{2} + \StokesDL[\sigma] \text{~~~~on~~~~} \Gamma$ \hfill $\kappa \sim 324$
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % $u = \StokesSL[\sigma] \text{~~~~on~~~~} \Gamma$ \hfill $\kappa \sim 651$
|
|
|
-
|
|
|
- % \vspace{1em}
|
|
|
- % $u = \frac{\sigma}{2} + \StokesDL[\sigma] + \StokesSL[\sigma] \text{~~~~on~~~~} \Gamma$ \hfill $\kappa \sim 9$
|
|
|
-
|
|
|
- % \end{columns}
|
|
|
-
|
|
|
- %\end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Mobility problem - combined field formulation}{} %<<<
|
|
|
-
|
|
|
- \only<1>{
|
|
|
- Represent fluid velocity: ~~$\displaystyle \vct{u} = \StokesSL[\vct{\nu}(\vct{F}_i, \vct{T}_i)] + \StokesCF[{\color{red}\vct{\sigma}} ] $
|
|
|
- }
|
|
|
- \only<2->{
|
|
|
- \vspace{-0.7em}
|
|
|
- Represent fluid velocity: ~~$\displaystyle \vct{u} = \StokesSL[\vct{\nu}(\vct{F}_i, \vct{T}_i)] + \StokesCF[{\color{red}\vct{\sigma}} - \sum_{i=1}^{6n} \mathfrak{v}_i \mathfrak{v}_i^T {\color{red}\vct{\sigma}} ] $
|
|
|
- }
|
|
|
-
|
|
|
- \only<1>{\vspace{0.5em}}%
|
|
|
- \only<2->{\vspace{-0.65em}}%
|
|
|
- and rigid body velocity: ~~$\displaystyle \vct{V} = -\sum_{i=1}^{6n} \mathfrak{v}_i \mathfrak{v}_i^T {\color{red}\vct{\sigma}}$
|
|
|
-
|
|
|
- \vspace{0.3em}
|
|
|
- where, ~$\displaystyle \StokesCF = \StokesDL + \StokesSL / (2 \varepsilon \log \varepsilon^{-1}) $.
|
|
|
-
|
|
|
-
|
|
|
- \only<3>{
|
|
|
- \vspace{2.5em}
|
|
|
- Applying boundary conditions,
|
|
|
-
|
|
|
- \vspace{0.3em}
|
|
|
- \qquad$\qquad\displaystyle
|
|
|
- (I/2 + K) \, \left( {\color{red}\vct{\sigma}} - \sum_{i=1}^{6n} \mathfrak{v}_i \mathfrak{v}_i^T {\color{red}\vct{\sigma}} \right) + \sum_{i=1}^{6n} \mathfrak{v}_i \mathfrak{v}_i^T {\color{red}\vct{\sigma}} = \vct{u}_s - S \, \vct{\nu}
|
|
|
- $
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- Second kind integral equation and well-conditioned!
|
|
|
- }
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - Sedimentation Flow}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1.5em}
|
|
|
- \begin{columns}[t]
|
|
|
- \column{0.7\textwidth}
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf Time-stepping:} 5-th order adaptive SDC
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf 8-digits accuracy} in quadratures, GMRES solve, \\
|
|
|
- and time-stepping.
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf 40 CPU cores}
|
|
|
-
|
|
|
- \only<2>{
|
|
|
- \embedvideo{\includegraphics[width=0.99\textwidth]{videos/sed2-top-zoom1}}{videos/sed2-top-zoom1.avi}
|
|
|
- }
|
|
|
-
|
|
|
- \column{0.4\textwidth}
|
|
|
- \vspace{-0.5em}
|
|
|
- \only<1>{
|
|
|
- \embedvideo{\includegraphics[width=0.99\textwidth]{videos/sed2-side-color}}{videos/sed2-side-color.mov}
|
|
|
- }
|
|
|
- \only<2>{
|
|
|
- \includegraphics[width=0.99\textwidth]{videos/sed2-side-color}
|
|
|
- }
|
|
|
-
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- %\embedvideo{\includegraphics[width=0.25\textwidth]{videos/mesh}}{videos/mesh.avi}
|
|
|
- % 5-th order SDC time-stepping
|
|
|
- % 7 - digits accuracy
|
|
|
- % adaptively refined mesh
|
|
|
-
|
|
|
- % block diagonal preconditioner - plot of GMRES iterations
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - Sedimentation Flow}{} %<<<
|
|
|
-
|
|
|
- \vspace{-2.0em}
|
|
|
- \begin{center}
|
|
|
- \resizebox{0.85\textwidth}{!}{\begin{tikzpicture}
|
|
|
- \pgfplotsset{
|
|
|
- xmin=0, xmax=250,
|
|
|
- width=12cm, height=7cm,
|
|
|
- xlabel={$T$}, xtick distance=50,
|
|
|
- }
|
|
|
- \begin{axis}[ymin=0, ymax=110, ylabel={$N_{iter}$}, legend style={draw=none,at={(0,1)},anchor=north west}]
|
|
|
- \addplot [thick,color=blue] table [x={t},y={noprecond}] {data/sed2}; \addlegendentry{no-preconditioner};
|
|
|
- \addplot [thick,color=red] table [x={t},y={precond}] {data/sed2}; \addlegendentry{block-preconditioner};
|
|
|
- %\addplot [thick,color=green] table [x={t},y={KSPprecond}] {data/sed2}; \addlegendentry{Krylov-preconditioner};
|
|
|
- \end{axis}
|
|
|
-
|
|
|
- \begin{axis}[axis y line*=right, ymin=0, ymax=65000, ylabel={$N$}, legend style={draw=none,at={(0.97,0.97)},anchor=north east}]
|
|
|
- \addplot [thick,dashed,color=black] table [x={t},y={N}] {data/sed2}; \addlegendentry{$N$};
|
|
|
- \end{axis}
|
|
|
- \end{tikzpicture}}
|
|
|
- \end{center}
|
|
|
-
|
|
|
- \vspace{-1em}
|
|
|
- {\bf Close-to-touching:} ~~smaller time-steps, ~~more unknowns ($N$), \\
|
|
|
- high GMRES iteration count (one-body preconditioner doesn't help). \\
|
|
|
- {\color{red} $\sim 125 \times$ more expensive!}
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Accelerating GMRES Solves}{} %<<<
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \resizebox{.9\textwidth}{!}{\begin{tikzpicture}%<<<
|
|
|
- % draw horizontal line
|
|
|
- \draw[ultra thick, ->] (0,0) -- (14,0);
|
|
|
-
|
|
|
- % draw vertical lines
|
|
|
- \foreach \x in {2,4,6,8,10,12}
|
|
|
- \draw[ultra thick] (\x cm,3pt) -- (\x cm,-3pt);
|
|
|
-
|
|
|
- % draw node
|
|
|
- \draw[ultra thick] ( 4,0) node[below=3pt] {$t_{n-2}$};
|
|
|
- \draw[ultra thick] ( 6,0) node[below=3pt] {$t_{n-1}$};
|
|
|
- \draw[ultra thick] ( 8,0) node[below=3pt] {$t_{n}$};
|
|
|
- \draw[ultra thick] (10,0) node[below=3pt] {$t_{n+1}$};
|
|
|
- \end{tikzpicture}}%>>>
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \begin{itemize}
|
|
|
- \setlength\itemsep{0.5em}
|
|
|
- \item Forward Euler: ~$n\text{-}{th}$~ time step
|
|
|
- \begin{itemize}
|
|
|
- \item solve BIE using GMRES:~~ $A_{y_n} \sigma_{\!n} = b_{y_n}$
|
|
|
- \item advance to $t_{n+1}$:~~~ $y_{n+1} = y_{n} + h\, v(\sigma_{\!n})$
|
|
|
- \end{itemize}
|
|
|
- \only<2->{\item Use ~$\sigma_{\!n-1}$~ as initial guess to GMRES}
|
|
|
- \only<3->{: {\color{red} doesn't work well}}
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \only<4->{
|
|
|
- \vspace{0.5em}
|
|
|
- \begin{itemize}
|
|
|
- \item Re-use Krylov subspace from previous time step?
|
|
|
-
|
|
|
- \only<5->{
|
|
|
- \begin{itemize}
|
|
|
- \item Krylov subspace: ~~$X \leftarrow [b, ~A b, ~\cdots, ~A^{k\shortminus\!1} b]$
|
|
|
-
|
|
|
- \item Compute QR decomposition: ~ $QR \leftarrow AX$
|
|
|
-
|
|
|
- \item Preconditioner: ~ $P \coloneq I - Q Q^{T} + X R^{-1} Q^{T}$
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \item[] \qquad $P \, Ax = x$ \quad for all~~ $x \in span(X)$
|
|
|
- \item[] \qquad ~\, $P \, y = y$ \quad for all~~ $y \perp span(X)$
|
|
|
-
|
|
|
- \end{itemize}
|
|
|
- }
|
|
|
- \end{itemize}}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Krylov Preconditioning with SDC}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1em}
|
|
|
- \resizebox{.9\textwidth}{!}{\begin{tikzpicture}%<<<
|
|
|
- % draw horizontal line
|
|
|
- \draw[ultra thick, ->] (0,0) -- (14,0);
|
|
|
-
|
|
|
- % draw vertical lines
|
|
|
- \foreach \x in {1.7, 12.3}
|
|
|
- \draw[ultra thick] (\x cm,6pt) -- (\x cm,-6pt);
|
|
|
- \draw[ultra thick] (1.7000 ,0) node[above=5pt] {$a$};
|
|
|
- \draw[ultra thick] (12.3000,0) node[above=5pt] {$b$};
|
|
|
-
|
|
|
- \foreach \x in {1.9000, 2.6699, 4.5000, 7.0000, 9.5000, 11.3301, 12.1000}
|
|
|
- \draw[ultra thick, blue] (\x cm,3pt) -- (\x cm,-3pt);
|
|
|
-
|
|
|
- % draw node
|
|
|
- \draw[ultra thick, blue] (1.9000 ,0) node[below=3pt] {$t_1$};
|
|
|
- \draw[ultra thick, blue] (2.6699 ,0) node[below=3pt] {$t_2$};
|
|
|
- \draw[ultra thick, blue] (4.5000 ,0) node[below=3pt] {$t_3$};
|
|
|
- %\draw[ultra thick, blue] (7.0000 ,0) node[below=3pt] {$t_4$};
|
|
|
- %\draw[ultra thick, blue] (9.5000 ,0) node[below=3pt] {$t_5$};
|
|
|
- \draw[ultra thick, blue] (8.5,0) node[below=3pt] {$\cdots$};
|
|
|
- %\draw[ultra thick, blue] (11.3301,0) node[below=3pt] {$t_6$};
|
|
|
- \draw[ultra thick, blue] (12.1000,0) node[below=3pt] {$t_m$};
|
|
|
-
|
|
|
- \only<2->{%<<<
|
|
|
- \draw[ultra thick, DarkGreen] (1.9000 ,-1) node {$P_1$};
|
|
|
- \draw[ultra thick, DarkGreen] (2.6699 ,-1) node {$P_2$};
|
|
|
- \draw[ultra thick, DarkGreen] (4.5000 ,-1) node {$P_3$};
|
|
|
- \draw[ultra thick, DarkGreen] (8.5000 ,-1) node {$\cdots$};
|
|
|
- \draw[ultra thick, DarkGreen] (12.1000,-1) node {$P_m$};
|
|
|
-
|
|
|
- \draw[ultra thick, DarkGreen, ->] (2.10 ,-1) -- (2.40 ,-1);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (3.00 ,-1) -- (3.50 ,-1);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (4.86 ,-1) -- (5.40 ,-1);
|
|
|
- }%>>>
|
|
|
- \only<3->{%<<<
|
|
|
- \draw[ultra thick, DarkGreen, ->] (1.9000 ,-1.25) -- (1.9000 ,-1.8);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (2.6699 ,-1.25) -- (2.6699 ,-1.8);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (4.5000 ,-1.25) -- (4.5000 ,-1.8);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (12.100 ,-1.25) -- (12.100 ,-1.8);
|
|
|
-
|
|
|
- \draw[ultra thick, DarkGreen] (1.9000 ,-2.1) node {~~\,$P^{(1)}_1$};
|
|
|
- \draw[ultra thick, DarkGreen] (2.6699 ,-2.1) node {~~\,$P^{(1)}_2$};
|
|
|
- \draw[ultra thick, DarkGreen] (4.5000 ,-2.1) node {~~\,$P^{(1)}_3$};
|
|
|
- \draw[ultra thick, DarkGreen] (8.5000 ,-2.1) node {$\cdots$};
|
|
|
- \draw[ultra thick, DarkGreen] (12.100 ,-2.1) node {~~\,$P^{(1)}_m$};
|
|
|
-
|
|
|
- \draw[ultra thick, black, ->] (0.75 ,-0.5) -- (0.75 ,-3.5);
|
|
|
- \draw[ultra thick, black] (0.5,-2) node[rotate=-90] {corrections};
|
|
|
- }%>>>
|
|
|
- \only<4->{%<<<
|
|
|
- \draw[ultra thick, DarkGreen, ->] (1.9000 ,-2.5) -- (1.9000 ,-3.0);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (2.6699 ,-2.5) -- (2.6699 ,-3.0);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (4.5000 ,-2.5) -- (4.5000 ,-3.0);
|
|
|
- \draw[ultra thick, DarkGreen, ->] (12.100 ,-2.5) -- (12.100 ,-3.0);
|
|
|
-
|
|
|
- \draw[ultra thick, DarkGreen] (1.9000 ,-3.3) node {~~\,$P^{(2)}_1$};
|
|
|
- \draw[ultra thick, DarkGreen] (2.6699 ,-3.3) node {~~\,$P^{(2)}_2$};
|
|
|
- \draw[ultra thick, DarkGreen] (4.5000 ,-3.3) node {~~\,$P^{(2)}_3$};
|
|
|
- \draw[ultra thick, DarkGreen] (8.5000 ,-3.3) node {$\cdots$};
|
|
|
- \draw[ultra thick, DarkGreen] (12.100 ,-3.3) node {~~\,$P^{(2)}_m$};
|
|
|
-
|
|
|
- %\draw[ultra thick, DarkGreen, ->] (1.9000 ,-3.7) -- (1.9000 ,-4.2);
|
|
|
- %\draw[ultra thick, DarkGreen, ->] (2.6699 ,-3.7) -- (2.6699 ,-4.2);
|
|
|
- %\draw[ultra thick, DarkGreen, ->] (4.5000 ,-3.7) -- (4.5000 ,-4.2);
|
|
|
- %\draw[ultra thick, DarkGreen, ->] (12.100 ,-3.7) -- (12.100 ,-4.2);
|
|
|
- }%>>>
|
|
|
-
|
|
|
- \end{tikzpicture}}%>>>
|
|
|
-
|
|
|
- \only<5->{
|
|
|
- \vspace{1.4em}
|
|
|
-
|
|
|
- \begin{columns}
|
|
|
- \column{0.05\textwidth}
|
|
|
- \column{0.45\textwidth}
|
|
|
- GMRES iter without preconditioner:
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \begin{tabular}{r | r r r r r}
|
|
|
- \parbox[t]{2mm}{\multirow{5}{*}{\rotatebox[origin=c]{-90}{correction $\rightarrow$}}}
|
|
|
- & \multicolumn{5}{c}{sub-step $\rightarrow$} \\
|
|
|
- \hline
|
|
|
- & 66 & 66 & 66 & 66 & 66 \\
|
|
|
- & 66 & 66 & 66 & 66 & 66 \\
|
|
|
- & 66 & 66 & 66 & 66 & 66 \\
|
|
|
- & 66 & 66 & 66 & 66 & 66 \\
|
|
|
- \end{tabular}
|
|
|
-
|
|
|
- \column{0.05\textwidth}
|
|
|
- \column{0.44\textwidth}
|
|
|
- \only<6->{
|
|
|
- GMRES iter with preconditioner:
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \begin{tabular}{r | r r r r r}
|
|
|
- \parbox[t]{2mm}{\multirow{5}{*}{\rotatebox[origin=c]{-90}{correction $\rightarrow$}}}
|
|
|
- & \multicolumn{5}{c}{sub-step $\rightarrow$} \\
|
|
|
- \hline
|
|
|
- & 66 & 30 & 22 & 45 & 30 \\
|
|
|
- & 35 & 17 & 33 & 28 & 24 \\
|
|
|
- & 8 & 4 & 14 & 5 & 12 \\
|
|
|
- & 1 & 1 & 2 & 2 & 4 \\
|
|
|
- \end{tabular}}
|
|
|
-
|
|
|
- \end{columns}
|
|
|
- }
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - Sedimentation Flow}{} %<<<
|
|
|
-
|
|
|
- \vspace{-2.0em}
|
|
|
- \begin{center}
|
|
|
- \resizebox{0.95\textwidth}{!}{\begin{tikzpicture}
|
|
|
- \pgfplotsset{
|
|
|
- xmin=0, xmax=250,
|
|
|
- width=12cm, height=7cm,
|
|
|
- xlabel={$T$}, xtick distance=50,
|
|
|
- }
|
|
|
- \begin{axis}[ymin=0, ymax=110, ylabel={$N_{iter}$}, legend style={draw=none,at={(0,1)},anchor=north west}]
|
|
|
- \addplot [thick,color=blue] table [x={t},y={noprecond}] {data/sed2}; \addlegendentry{no-preconditioner};
|
|
|
- \addplot [thick,color=red] table [x={t},y={precond}] {data/sed2}; \addlegendentry{block-preconditioner};
|
|
|
- \addplot [thick,color=DarkGreen] table [x={t},y={KSPprecond}] {data/sed2}; \addlegendentry{Krylov-preconditioner};
|
|
|
- \end{axis}
|
|
|
-
|
|
|
- \begin{axis}[axis y line*=right, ymin=0, ymax=65000, ylabel={$N$}, legend style={draw=none,at={(0.97,0.97)},anchor=north east}]
|
|
|
- \addplot [thick,dashed,color=black] table [x={t},y={N}] {data/sed2}; \addlegendentry{$N$};
|
|
|
- \end{axis}
|
|
|
- \end{tikzpicture}}
|
|
|
- \end{center}
|
|
|
-
|
|
|
- %\vspace{-1em}
|
|
|
- %{\bf Close-to-touching:} ~~smaller time-steps, ~~more unknowns ($N$), \\
|
|
|
- %high GMRES iteration count (block preconditioner doesn't help). \\
|
|
|
- %{\color{red} $\sim 125 \times$ more expensive!}
|
|
|
- \end{FIframe} %>>>
|
|
|
- %>>>
|
|
|
-
|
|
|
-
|
|
|
- %<<< Sedimentation flow
|
|
|
- \begin{FIframe}{Numerical Results - Sedimentation Flow}{} %<<<
|
|
|
-
|
|
|
- \begin{columns}
|
|
|
-
|
|
|
- \column{0.35\textwidth}
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf 5-th order adaptive SDC}
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf 8-digits accuracy} in quadratures, GMRES solve, \\
|
|
|
- and time-stepping.
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf 0.5 million unknowns} \\
|
|
|
- 64 rings.
|
|
|
-
|
|
|
- \vspace{1ex}
|
|
|
- {\bf 160 CPU cores}
|
|
|
-
|
|
|
- \column{0.65\textwidth}
|
|
|
-
|
|
|
- \embedvideo{\includegraphics[width=0.99\textwidth]{videos/sed64}}{videos/sed64.mov}
|
|
|
-
|
|
|
- \end{columns}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
-
|
|
|
- \begin{FIframe}{Numerical Results - Sedimentation Flow}{} %<<<
|
|
|
-
|
|
|
- \vspace{-1.9em}
|
|
|
- \centering
|
|
|
- \only<1>{ \embedvideo{\includegraphics[width=0.94\textwidth]{videos/bacteria2_.png}}{videos/bacteria2_.mov} }%
|
|
|
- \only<2>{ \embedvideo{\includegraphics[width=0.47\textwidth]{videos/bacteria64-density.png}}{videos/bacteria64-density.mov} }
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
- %>>>
|
|
|
-
|
|
|
- \section{Software} %<<<
|
|
|
-
|
|
|
- \begin{frame}[t,fragile] \frametitle{CSBQ library}{} %<<<
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- {\bf Code:} ~~ {\color{blue} \url{https://github.com/dmalhotra/CSBQ}}
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- {\bf Requirements:} ~~ C++11 compiler ~~with~~ OpenMP 4.0
|
|
|
-
|
|
|
- \vspace{1em}
|
|
|
- {\bf Build system:} ~~ none (header only)
|
|
|
-
|
|
|
- \vspace{0.5em}
|
|
|
- \begin{minted}[
|
|
|
- %frame=lines,
|
|
|
- fontsize=\footnotesize,
|
|
|
- %linenos,
|
|
|
- gobble=0,
|
|
|
- mathescape
|
|
|
- ]{C++}
|
|
|
- #include <csbq.hpp>
|
|
|
- \end{minted}
|
|
|
-
|
|
|
-
|
|
|
- \vspace{3em}
|
|
|
- {\bf Optional dependencies:} ~~ BLAS, LAPACK, MPI, and PVFMM
|
|
|
-
|
|
|
- %\begin{itemize}
|
|
|
- %\item includes simple `Makefile' for example codes.
|
|
|
- %\end{itemize}
|
|
|
-
|
|
|
- \end{frame}
|
|
|
- %>>>
|
|
|
-
|
|
|
- \begin{frame} \frametitle{Library classes}{} %<<<
|
|
|
-
|
|
|
- \resizebox{1.05\linewidth}{!}{\begin{tikzpicture}
|
|
|
-
|
|
|
- \node[anchor=north west, draw=none, rounded corners=.45cm, minimum height=7cm, minimum width=15.2cm] at (-0.1,1.6) {};
|
|
|
-
|
|
|
- \only<3->{
|
|
|
- \node[anchor=north west, draw=blue,thick, rounded corners=.45cm] at (1.0,1.5) {\begin{tabular}{c} \bf Taylor states \end{tabular}};
|
|
|
- \node[anchor=north west, draw=blue,thick, rounded corners=.45cm] at (5.3,1.5) {\begin{tabular}{c} \bf Vacuum fields \end{tabular}};
|
|
|
- \node[anchor=north west, draw=blue,thick, rounded corners=.45cm] at (9.8,1.5) {\begin{tabular}{c} \bf Virtual casing \end{tabular}};
|
|
|
-
|
|
|
- \draw [line width=1mm] (0,0.25) -- (15.0,0.25);
|
|
|
- }
|
|
|
-
|
|
|
-
|
|
|
- \only<2->{
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.55cm] at (0,0) {\small
|
|
|
- \begin{tabular}{c}
|
|
|
- {\bf Surface} \\
|
|
|
- W7X, LHD, \\
|
|
|
- QAS3, etc, \\
|
|
|
- $(\mathbf{X}, \mathbf{Y}, \mathbf{Z})$
|
|
|
- \end{tabular}};
|
|
|
-
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.55cm] at (2.7,0) {\small
|
|
|
- \begin{tabular}{c}
|
|
|
- {\bf SurfaceOp} \\
|
|
|
- resample, $\mathbf{n}$, \\
|
|
|
- $\nabla_{\Gamma}$,~
|
|
|
- $\nabla_{\Gamma} \cdot$, \\
|
|
|
- $\nabla_{\Gamma} \times$,~
|
|
|
- $\Delta_{\Gamma}$,\\
|
|
|
- $\Delta^{-1}_{\Gamma}$
|
|
|
- \end{tabular}};
|
|
|
-
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.55cm] at (5.8,0) {\small
|
|
|
- \begin{tabular}{c}
|
|
|
- {\bf BoundaryIntegralOp}\\
|
|
|
- $\int\limits_\Gamma \sigma(\mathbf{r}') K(\mathbf{r}-\mathbf{r}') d a(\mathbf{r}')$
|
|
|
- \end{tabular}};
|
|
|
-
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.55cm] at (10.9,0) {\small
|
|
|
- \begin{tabular}{c}
|
|
|
- {\bf KernelFunction}\\
|
|
|
- Laplace, Helmholtz, \\
|
|
|
- Biot-Savart, etc.
|
|
|
- \end{tabular}};
|
|
|
- }
|
|
|
-
|
|
|
- \node[anchor=north west, draw=black,thick, rounded corners=.55cm] at (1,-3.3) {\small
|
|
|
- \begin{tabular}{c}
|
|
|
- {\bf SCTL:} Scientific Computing Template Library\\
|
|
|
- \hspace{30em} \\
|
|
|
- \\
|
|
|
- \end{tabular}};
|
|
|
-
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.45cm] at (2,-4.1) {\begin{tabular}{c} \bf Vector \end{tabular}};
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.45cm] at (5,-4.1) {\begin{tabular}{c} \bf Matrix \end{tabular}};
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.45cm] at (8,-4.1) {\begin{tabular}{c} \bf GMRES \end{tabular}};
|
|
|
- \node[anchor=north west, draw=red,thick, rounded corners=.45cm] at (11,-4.1) {\begin{tabular}{c} \bf FFT \end{tabular}};
|
|
|
-
|
|
|
- \end{tikzpicture}}
|
|
|
-
|
|
|
- \end{frame}%>>>
|
|
|
-
|
|
|
- %>>>
|
|
|
-
|
|
|
- \section{Conclusions} %<<<
|
|
|
-
|
|
|
- \begin{FIframe}{Conclusions}{} %<<<
|
|
|
-
|
|
|
- %\vspace{1.2em}
|
|
|
- \begin{itemize}
|
|
|
- \item Convergent boundary integral formulation for slender bodies.
|
|
|
- \begin{itemize}
|
|
|
- \item unlike SBT, boundary conditions are actually enforced to high accuracy.
|
|
|
- \end{itemize}
|
|
|
- \vspace{0.5ex}
|
|
|
- \item Special quadratures - efficient for aspect ratios as large as $10^5$.
|
|
|
- \begin{itemize}
|
|
|
- %\item fast computation of modal/toroidal Green's function.
|
|
|
- %\item special (Chebyshev) quadratures for singular integrals along length of fibers.
|
|
|
- \item quadrature setup rates up to $20,\!000$ unknowns/s/core (comparable to FMM speeds).
|
|
|
- \end{itemize}
|
|
|
- \vspace{0.5ex}
|
|
|
- \item Stokes mobility problem - combined field BIE formulation.
|
|
|
- \begin{itemize}
|
|
|
- \item well-conditioned formulation for slender-body geometries.
|
|
|
- \item high-order time stepping (SDC), Krylov subspace preconditioner.
|
|
|
- \end{itemize}
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \only<2>{
|
|
|
- \vspace{1.5em}
|
|
|
- {\bf Limitations and ongoing work:}
|
|
|
- \begin{itemize}
|
|
|
- \item Flexible fibers -- applications in biological fluids.
|
|
|
- \item Open problems: collision handling.
|
|
|
-
|
|
|
- %\item Open fibers (singularities at ends). %Special elements (and quadratures) for fiber endpoints (non-loop geometries).
|
|
|
- %%\item Replace Chebyshev quadratures with generalized Gaussian quadratures% of Bremer, Gimbutas and Rokhlin - SISC 2010.
|
|
|
- %%\item Parallelisation with proper load balancing.
|
|
|
- %%\item FMM acceleration of far-field computation.
|
|
|
- %%\item Apply to problems in biological fluids.
|
|
|
- %\item Mobility problem and flexible fibers.
|
|
|
- %\item Comparison w/ SBT efficiency when SBT is sufficiently accurate.
|
|
|
- \end{itemize}
|
|
|
- }
|
|
|
-
|
|
|
-
|
|
|
-
|
|
|
- % - end-caps so that we can have non-loop geometries
|
|
|
- % - replace Chebyshev quadratures with Generalized Gaussian Quadratures
|
|
|
- %%%%%%%% - develop preconditioners for close to touching geometries?
|
|
|
- % direct comparison with slender-body theory
|
|
|
- % develop applications ...
|
|
|
- % parallelization
|
|
|
-
|
|
|
-
|
|
|
-
|
|
|
- %\vspace{1em}
|
|
|
- %\textcolor{blue}{\bf Future directions}
|
|
|
-
|
|
|
- %\vspace{0.5em}
|
|
|
- %\begin{columns}
|
|
|
- % \column{0.9\textwidth}
|
|
|
- % \begin{itemize}
|
|
|
- % \item apply quadratures to numerical simulations of biological processes (collaboration with CCB).
|
|
|
- % \end{itemize}
|
|
|
- % \column{0.1\textwidth}
|
|
|
- %\end{columns}
|
|
|
-
|
|
|
- %\vspace{0.5em}
|
|
|
- %\begin{columns}
|
|
|
- % \column{0.65\textwidth}
|
|
|
- % \begin{itemize}
|
|
|
- % \item study convergence in close-to-touching setups; ~~ require adaptivity in length as well as $\theta$-dimensions.
|
|
|
- % \end{itemize}
|
|
|
- % \column{0.35\textwidth}
|
|
|
- % \includegraphics[width=0.9\textwidth]{figs/close-touching}
|
|
|
-
|
|
|
- % {\small (fig from Morse et al.)}
|
|
|
- %\end{columns}
|
|
|
-
|
|
|
- % - end-caps so that we can have non-loop geometries
|
|
|
- % - replace Chebyshev quadratures with Generalized Gaussian Quadratures
|
|
|
- %%%%%%%% - develop preconditioners for close to touching geometries?
|
|
|
- % direct comparison with slender-body theory
|
|
|
- % develop applications ...
|
|
|
- % parallelization
|
|
|
-
|
|
|
- %\vspace{0.75em}
|
|
|
- %\begin{columns}
|
|
|
- % \column{0.9\textwidth}
|
|
|
- % \begin{itemize}
|
|
|
- % \item develop similar ideas for other special cases and more generally for high aspect ratio panels
|
|
|
-
|
|
|
- % \begin{center}
|
|
|
- % \includegraphics[width=0.6\textwidth]{slender-body/high-aspect-panels.png}
|
|
|
- % \end{center}
|
|
|
- % \end{itemize}
|
|
|
- % \column{0.1\textwidth}
|
|
|
- %\end{columns}
|
|
|
-
|
|
|
- \end{FIframe} %>>>
|
|
|
+ \input{intro} % 3
|
|
|
+ \input{algo} % 7
|
|
|
+ \input{mobility} % 6
|
|
|
|
|
|
- %>>>
|
|
|
+ \input{software} % 8
|
|
|
|
|
|
+ \input{conclusions} % 1
|
|
|
|
|
|
\end{document}
|
|
|
|